証明問題で二等辺三角形があるとき
証明問題で二等辺三角形があるとき、
どの \(2\) 辺が等しい二等辺三角形なのか、情報が与えられます。
そのとき、
「二等辺三角形なので、底角は等しい」
は証明なしで使ってOKです。
どこが底角なのか、底角とは何か、一切説明する必要はありません。
例題1
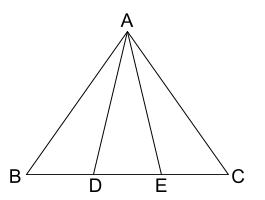
下の図で、\(\triangle ABC\) は \(AB=AC\) の二等辺三角形である。\(BC\) を \(3\) 等分する点を、\(D,E\) とするとき、\(AD=AE\) になることを証明せよ。
解説
三角形の合同を証明することで、その対応する辺が等しいことを言えます。
この証明の定番パターンは以前に学習していますね。
\(AD,AE\) をそれぞれ辺とする三角形を探しましょう。
そしてそれらは合同であると言えそうでしょうか?
\(\triangle ABD\) と \(\triangle ACE\) ですね!
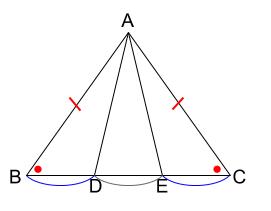
赤い角、辺は、\(\triangle ABC\) が二等辺三角形であることから言えます。
青い辺は仮定です。\(BC\) を \(3\) 等分しています。
つまり、\(2\) 辺とその間の角がそれぞれ等しいことから、合同が言えます!
解答
\(\triangle ABD\) と \(\triangle ACE\) において、
仮定より、\(BD=CE\) ・・・①
仮定より、\(AB=AC\) ・・・②
\(\triangle ABC\) は二等辺三角形なので、底角は等しいから
\(\angle ABD=\angle ACE\) ・・・③
①、②、③より、
\(2\) 辺とその間の角がそれぞれ等しいので、
\(\triangle ABD \equiv \triangle ACE\)
よって、合同な図形の対応する辺の長さは等しいので、
\(AD=AE\)
参考
\(AD=AE\) ということは、\(ADE\) が二等辺三角形であるということです。
つまり、
\(ADE\) が二等辺三角形であることを示し、
よって、\(AD=AE\) と結論に至る。
このような証明の流れもありです。
では、\(ADE\) が二等辺三角形であることはどうやって示せばいいのでしょうか。
底角が等しいことを示す以外ありえません。
\(\angle ADE=\angle AED\)
を示せれば、\(ADE\) が二等辺三角形であるといえます。
ではどうやって、\(\angle ADE=\angle AED\) を示すことができるか。
結局、\(\triangle ABD \equiv \triangle ACE\) から、その外角が等しいことをいう
しかないでしょう。
うーん・・・ずいぶん回り道ですね。
例題2
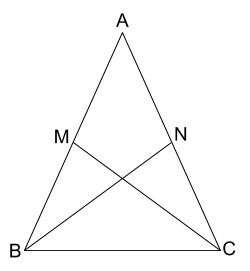
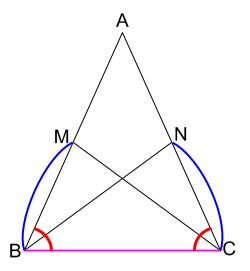
下の図のような \(AB=AC\) の二等辺三角形で、辺 \(AB,AC\) 中点を \(M,N\) とする。このとき、\(MC=NB\) を証明しなさい。
解説
最終目標の \(MC=NB\) 、ですが、
やはりこの \(2\) つが「合同な三角形の対応する辺」になっているはずです。
この解法が有力な第一候補です。
\(MC\) や \(NB\) を辺とする三角形は、\(\triangle MBC\) や \(\triangle NCB\) なので、
\(\triangle MBC\) ≡ \(\triangle NCB\)
が証明できればよさそうです。
合同条件にあてはまるかどうか、見ていきましょう。
\(MB=NC\) と \(\angle MBC=\angle NCB\) は
仮定である \(\triangle ABC\) が二等辺三角形であることからいえます。
また、辺 \(BC\) は共通なので、
以上で、\(2\) 辺とその間の角が等しいことから合同がいえます。
解答に仕上げましょう。
解答
\(\triangle MBC\) と \(\triangle NCB\) において、
\(MB=AB×\displaystyle \frac{1}{2}\) ・・・①
\(NC=AC×\displaystyle \frac{1}{2}\) ・・・②
仮定より、\(AB=AC\) なので、①、②より、
\(MB=NC\) ・・・③
\(\triangle ABC\) は二等辺三角形なので、底角は等しいから
\(\angle MBC=\angle NCB\) ・・・④
共通なので、\(BC=CB\)・・・⑤
③、④、⑤より、
\(2\) 辺とその間の角がそれぞれ等しいので、
\(\triangle MBC \equiv \triangle NCB\)
よって、合同な図形の対応する辺の長さは等しいので、
\(MC=NB\)
参考
\(MC\) や \(NB\) を辺とする三角形は、
\(\triangle AMC\) や \(\triangle ANB\)
もあります。
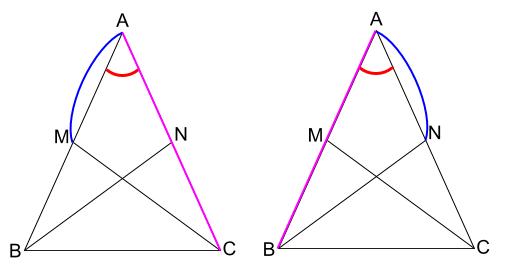
\(\triangle AMC\) ≡ \(\triangle ANB\)
が証明できれば、それでOKです。
証明できそうでしょうか?
\(AB=AC\) と \(AM=AN\) は仮定
\(\angle A\) は共通
より、\(2\) 辺とその間の角がそれぞれ等しいことから合同がいえますね。
こちらから証明しても立派な別解です。