例題
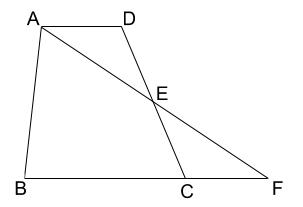
\(AD /\!/ BC\) の台形\(ABCD\) の辺 \(DC\) の中点を \(E\) とし、\(AE\) の延長線と \(BC\) の延長線との交点を \(F\) とする。このとき、\(AD=FC\) となることを証明しなさい。
解説
今までに見たことのないパターンですね。
\(2\) つの線分の長さが等しいことを証明しなくてはなりません。
どうやって証明すればいいのか・・・
これも結局「三角形の合同」を証明すれば良いのです。
三角形アイウと三角形カキクが合同ならば、
辺アイと辺カキの長さは等しいといえます。
「合同な三角形の対応する辺の長さは等しいから」
です。
これを利用します。
三角形の合同を考える
例題で示したいのは、\(AD=FC\) です。
この \(2\) つが、「合同な三角形の対応する辺」になっているはずです。
そのような、解き方を知っている状態で図を見るのです。
すると・・・見えますね!
\(\triangle ADE\) と \(\triangle FCE\) が合同ですね!
辺の長さが等しい箇所
角の大きさが等しい箇所
をチェックしていきましょう。
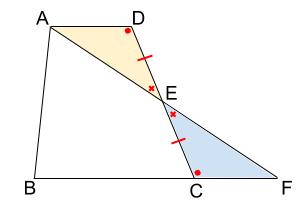
\(1\) 辺とその両端の角が等しいことから、合同といえます!
証明の骨組み
\(\triangle ADE\) と \(\triangle FCE\) が合同であることを証明する。
証明をしたら、下の結びの文をかいて証明終了。
よって、合同な三角形の対応する辺の長さは等しいので、\(AD=FC\)
ではいきましょう!
解答
\(\triangle ADE\) と \(\triangle FCE\) において、
仮定より、\(DE=CE\)・・・①
対頂角は等しいので、\(\angle DEA=\angle CEF\)・・・②
平行線の錯角は等しいので、\(\angle ADE=\angle FCE\)・・・③
①、②、③より、\(1\) 辺とその両端の角が等しいので、\(\triangle ADE \equiv \triangle FCE\)
よって、合同な三角形の対応する辺の長さは等しいので、\(AD=FC\)
