内角の和
三角形の内角の和は \(180°\)
四角形の内角の和は \(360°\)
これは小学校で学習しましたし、暗記もできていることと思います。
では、
五角形の内角の和は何度でしょうか。
六角形の内角の和は何度でしょうか。
七角形の内角の和は何度でしょうか。
\(N\) 角形の内角の和は何度でしょうか。
まず結論を書いてしまいますが、
\(N\) 角形の内角の和は、\(180×(N-2)°\)
多角形の内角の和
実際に内角の和をだしてみましょう。
\(N\) 角形の内角の和は、\(180×(N-2)°\)
より、
五角形の内角の和は、\(180×(5-2)=540°\)
六角形の内角の和は、\(180×(6-2)=720°\)
七角形の内角の和は、\(180×(7-2)=900°\)
となります。
では、なぜこの公式が成立するのでしょうか。
三角形に分割する
\(N\) 角形は\((N-2)\) 個の三角形に分割することができます。
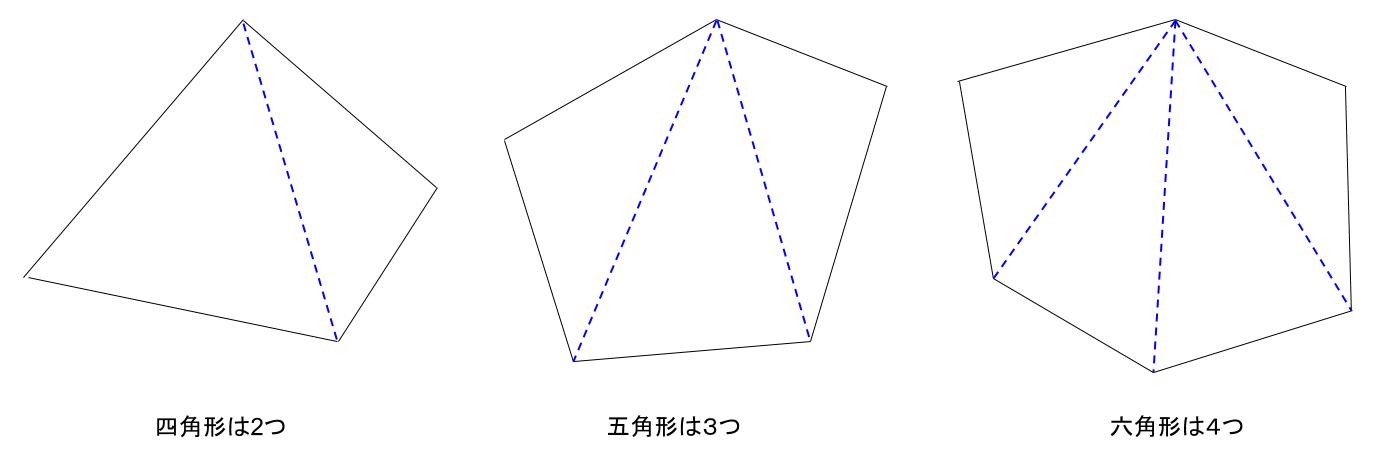
よって、その内角の和は、分割された三角形の内角の和に等しいので、
\(N\) 角形の内角の和は、\(180×(N-2)°\)
が成立します。
中心の1点から、三角形に分割する
内部の1点を用いて、\(N\) 角形を三角形に分割します。
内部の点は、どこであっても構いません。
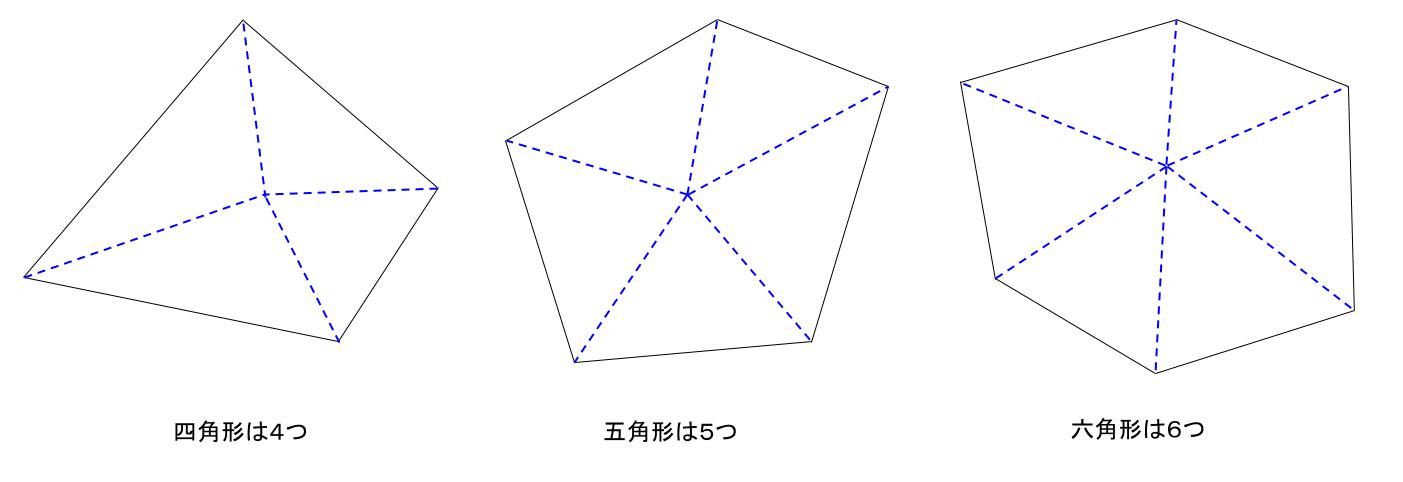
\(N\) 角形には、\(N\) 個の辺があるので、この分割では必ず、
「\(N\) 角形は \(N\) 個の三角形に分割される」
が成り立ちます。
この \(N\) 個の三角形の内角の和は、
\(180×N°\) となりますが、
\(N\) 角形の内角の和には、中心の \(360°\) がよけいです。
よって、
\(180N-360=180N-180×2=180×(N-2)\)
これで示せました。
外角の和
あらゆる多角形の外角の和は、\(360°\) です。
\(N\) 角形の外角の和を出すとき、外角は下図のような、時計回りの \(N\) 個を選ぶか、
反時計まわりの \(N\) 個を選びます。
どちらか片方だけの \(N\) 個の和をとります。
そして、それは、必ず \(360°\) になるのです。
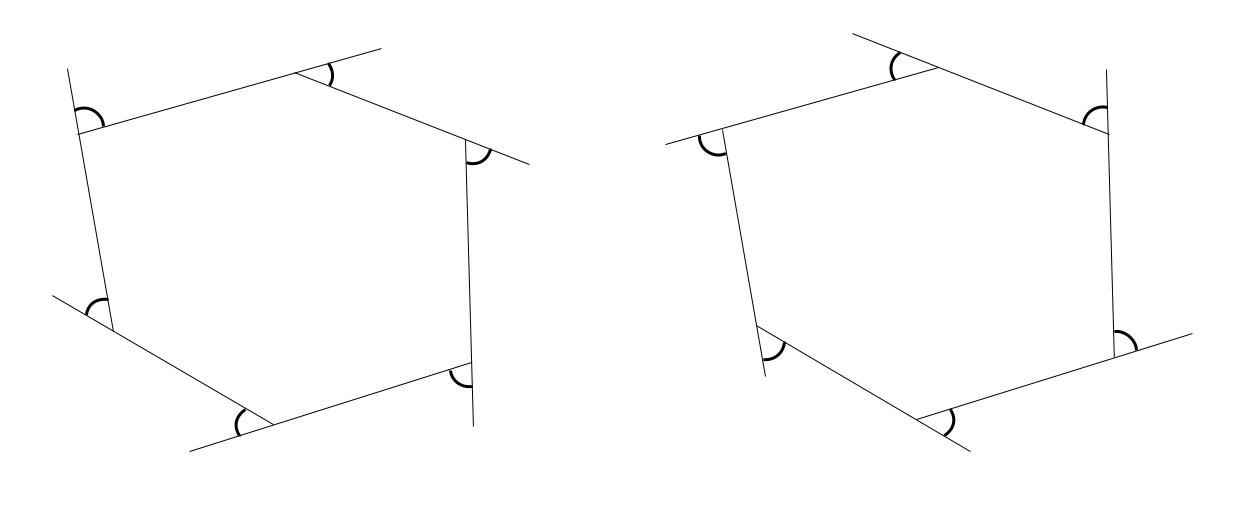
では、なぜこのことが成立するのでしょうか。
直感的説明 ぐるっと1周だから360°
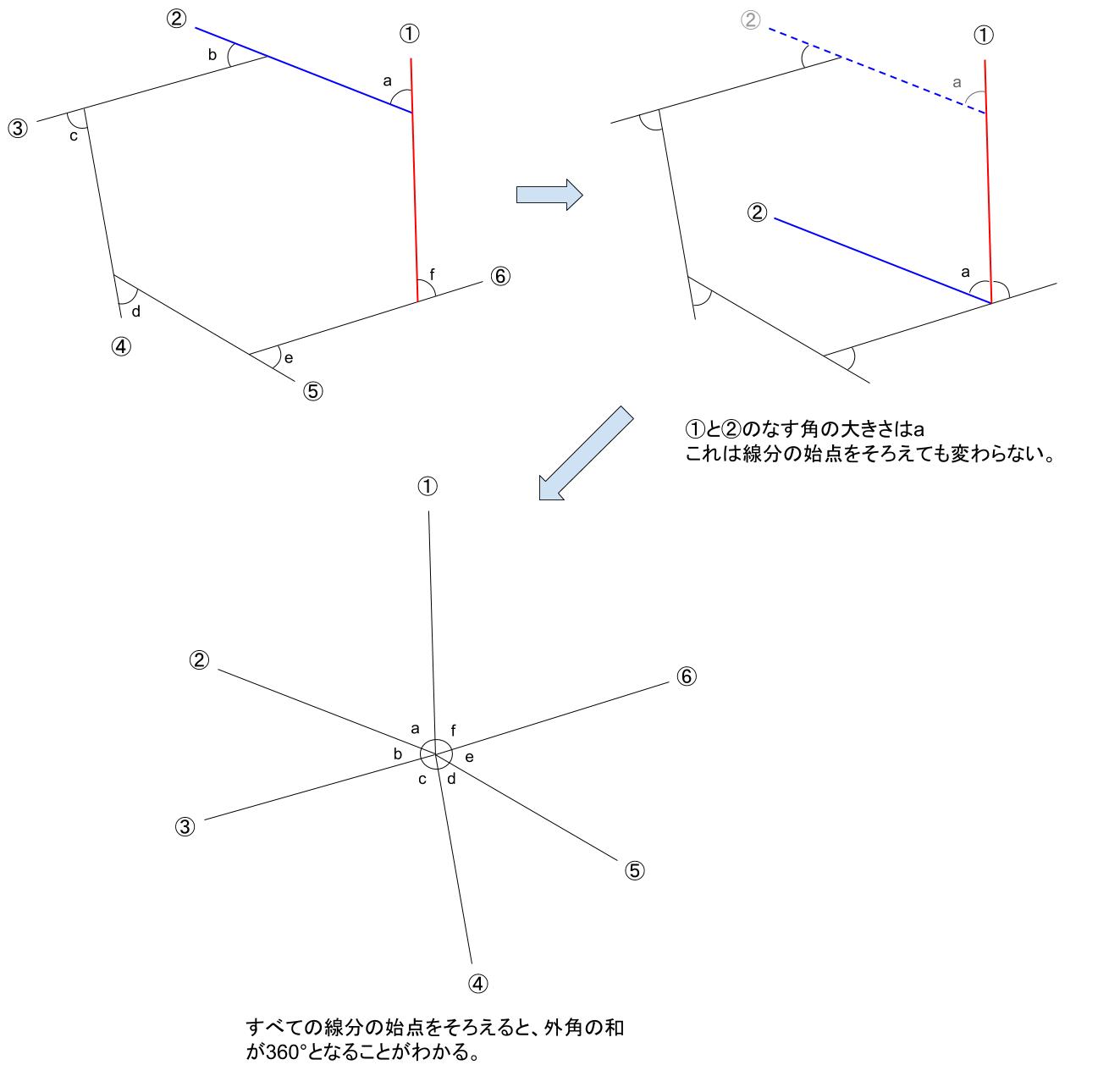
数式で説明
\(N\) 角形には、\(180°\) が \(N\) 個あることがわかります。
このうち、\(N\) 角形の内角の和の分を引けば、ちょうど \(N\) 角形の外角の和が求まることになります。
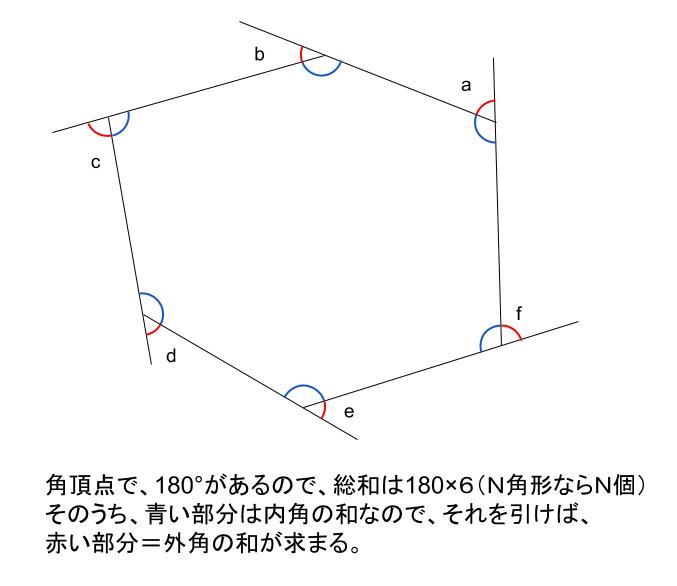
\(N\) 角形の \(N\) 個の頂点に、\(180°\) がありその総和は
\(180×N\)
ここから、\(N\) 角形の内角の和、\(180×(N-2)\) をひくので、
\(180×N-180×(N-2)=360°\)
これで示すことができました。
スポンサーリンク
