\(\triangle ABC\) が二等辺三角形であることを証明せよ
三角形が二等辺三角形であることを示したいとき、
・\(2\) つの辺が等しい
・\(2\) つの角が等しい
のどちらか片方がいえればOKです。
これも暗記ですよ。
三角形の合同条件を暗記したの同じように。
例題1
\(AD /\!/ BC\) の台形 \(ABCD\) の辺 \(AB\) 上に、\(AD=AE\) となる点 \(E\) をとった。
\(DE\) の延長線と \(CB\) の 延長線の交わる点を \(F\) とするとき、\(\triangle BEF\) が二等辺三角形であることを証明せよ。
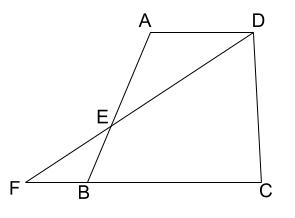
解説
\(\triangle BEF\) は見た感じ二等辺三角形ですが、どのように証明したらよいのでしょうか。
・\(2\) つの辺が等しい
・\(2\) つの角が等しい
のいずれかがいえればよいのです。
よって、等しい辺や角の情報を図に入れていきましょう。
\(AD=AE\) なので、\(\triangle AED\) が二等辺三角形で、
その底角(青い角)が等しいです。
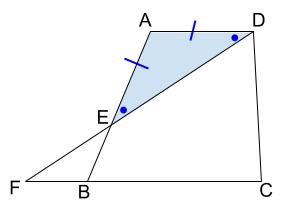
平行線があれば、等しい角の情報です。
\(AD /\!/ BC\) なので、錯角が等しいです。
もちろん対頂角も等しいです。
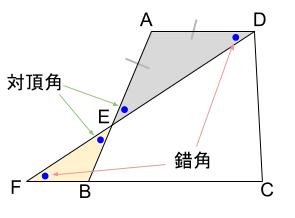
\(\triangle BEF\) は \(2\) つの角が等しいので、二等辺三角形であることがいえます。
これを解答にします。
角度が等しいことをていねいに順序立てて説明します。
解答
仮定 \(AD=AE\) より、\(\triangle AED\) は二等辺三角形である。
二等辺三角形の底角は等しいので、\(\angle AED=\angle ADE\) ・・・①
対頂角なので、\(\angle AED=\angle BEF\) ・・・②
仮定\(AD /\!/ BC\) より、平行線の錯角は等しいので、
\(\angle ADE=\angle BFE\) ・・・③
①、②より、\(\angle ADE=\angle BEF\) ・・・④
③、④より、\(\angle BFE=\angle BEF\)
よって、\(2\) つの角が等しいので、\(\triangle BEF\) は二等辺三角形である。
例題2
下の図のような、\(AB=AC\) の二等辺三角形で、辺 \(AB,AC\) 上に、\(DB=EC\) となる点\(D,E\) をとった。このとき、\(\triangle FBC\) が二等辺三角形であることを証明せよ。
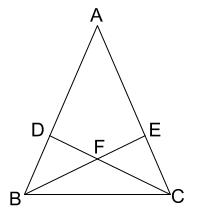
解説
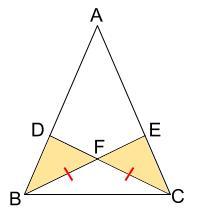
\(2\) つの辺が等しいから証明ならば
\(FB=FC\) から証明するとなると、
下図のクリーム色の三角形の合同をいう必要があります。
簡単には言えなさそうですね・・・
\(2\) つの角が等しいから証明ならば
\(\angle FBC=\angle FCB\) から証明するとなると、
\(\triangle DBC \equiv \triangle ECB\) を言う必要があります。
これは、できそうです。\(DB=EC\) が与えられてますし。
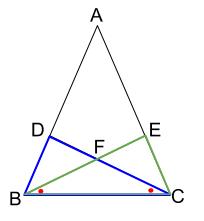
より、\(\triangle DBC \equiv \triangle ECB\) を目標に、
等しい辺、角の情報を図に入れていきましょう。
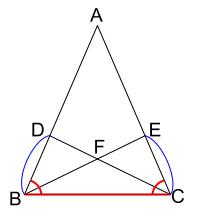
\(2\) 辺とその間の角がそれぞれ等しいことから、
\(\triangle DBC \equiv \triangle ECB\) がいえますね。
これを解答にまとめます。
解答
\(\triangle DBC\) と \( \triangle ECB\) において
仮定より、\(DB=EC\) ・・・①
共通なので、\(BC=CB\) ・・・②
二等辺三角形の底角は等しいので、
\(\angle DBC=\angle ECB\) ・・・③
①.②、③より、\(2\) 辺とその間の角がそれぞれ等しいことから、
\(\triangle DBC \equiv \triangle ECB\)
合同な図形の対応する角の大きさは等しいので、
\(\angle FCB=\angle FBC\)
よって、\(2\) つの角が等しいので、\(\triangle FBC\) は二等辺三角形である。
