例題
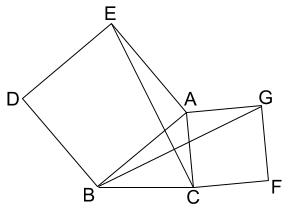
下の図のように、\(\triangle ABC\) の辺\(AB,AC\) を \(1\) 辺とする正方形\(DBAE\) と正方形\(ACFG\) がある。このとき、\(EC=BG\) であることを証明しなさい。
解説
証明の概略を考察
\(2\) つの線分の長さが等しいことの証明です。
前問の通り、これも結局「三角形の合同」を証明すれば良いのです。
示したいのは、\(EC=BG\) です。
この \(2\) つが、「合同な三角形の対応する辺」になっているはずです。
\(\triangle AEC\) と\(\triangle ABG\) が合同であることが予想されますね!
この \(2\) つの三角形の
辺の長さが等しい箇所
角の大きさが等しい箇所
をチェックしていきましょう。
正方形があるので、等しい辺はすぐにわかります。
赤い辺どうし、青い辺どうしが等しい長さです。
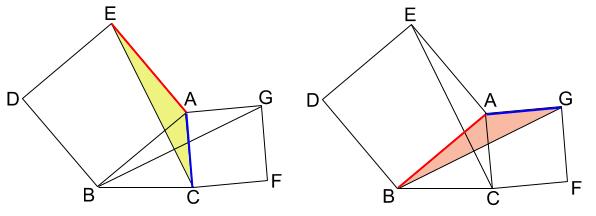
\(2\) つの辺がそれぞれ等しいので、
あとは、「その間の角が等しい」が言えればOKです。
どちらの三角形も、赤い辺と青い辺の間の角は
直角+●です。
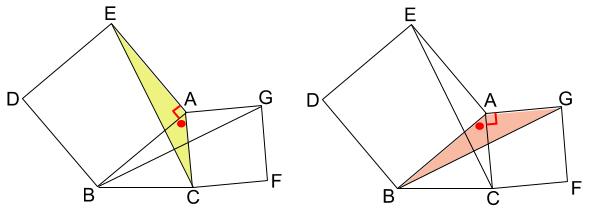
以上より、\(2\) 辺とその間の角がそれぞれ等しいことから、合同といえます!
解答
\(\triangle AEC\) と\(\triangle ABG\) において
仮定より、正方形 \(DBAE\) の辺なので、\(AE=AB\)・・・①
仮定より、正方形 \(ACFG\) の辺なので、\(CA=GA\)・・・②
また、\(\angle CAE=\angle BAC+\angle EAB=\angle BAC+90°\)・・・③
\(\angle GAB=\angle BAC+\angle CAG=\angle BAC+90°\)・・・④
③、④より、
\(\angle CAE=\angle GAB\)・・・⑤
①、②、⑤より、\(2\) 辺とその間の角がそれぞれ等しいので
\(\triangle AEC \equiv \triangle ABG\)
合同な図形の対応する辺の長さは等しいので、\(EC=BG\)
