例題1
\(1,2,3,4\) の \(4\) 枚のカードがある。この中から連続して \(2\) 枚を引き、\(1\) つを十の位の数、もう \(1\) つを一の位の数として \(2\) けたの数をつくる。
このとき次の確率を求めなさい。
① できた数が、奇数である確率
② できた数が、\(3\) の倍数である確率
解説
当然、樹形図をかきます。
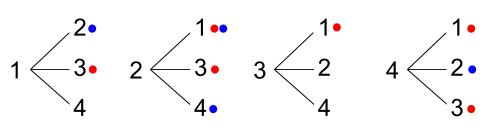
すべての場合の数は、\(12\) 通りです。
① できた数が、奇数である確率
奇数になるのは赤丸の \(6\) 通りです。
よって、求める確率は、\(\displaystyle \frac{6}{12}=\displaystyle \frac{1}{2}\) です。
できた数が、3の倍数である確率
②\(3\) の倍数になるのは青丸の \(4\) 通りです。
よって、求める確率は、\(\displaystyle \frac{4}{12}=\displaystyle \frac{1}{3}\) です。
例題2
\(1,2,3,4,5\) の \(5\) 枚のカードが箱の中にある。この箱の中から \(1\) 枚を引き、箱の中に戻します。続いて箱の中から \(1\) 枚を引きます。はじめに引いたカードにかいてあった数を十の位、次に引いたカードにかいてあった数を一の位として \(2\) けたの数をつくるとき、できた \(2\) けたの数が \(3\) の倍数である確率を求めなさい。
解説
当然、樹形図をかきます。
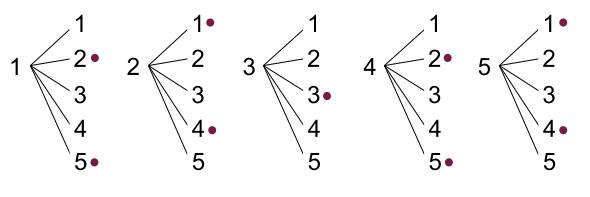
すべての場合の数は、\(5×5=25\) 通りです。
\(3\) の倍数になるのは●丸の \(9\) 通りなので
よって、求める確率は、\(\displaystyle \frac{9}{25}\) です。
考察
\(25\) 通りの書き出しをするくらい嫌がっていてはいけません。
しかし、ある程度書き出しに慣れてきたら、省略できるところは省略して構いません。
たとえば、すべての場合の数は、\(25\) 通りが、\(5×5=25\) と求まることが確信を持てるのならば、上の樹形図の全書き出しをしなくてもよいでしょう。
どうしたら確信が持てるのか?
樹形図の書き出しをたくさん経験することによって、「上の樹形図が頭の中に描ける能力を持つ」ことができたらです。
結局、樹形図以外の解法がありません。それを肝に銘じてください。
その後は \(3\) の倍数の書き出しです。
\(12,15,21,24,33,42,45,51,54\) と順に書き出しをします。
これは省略できません。
スポンサーリンク
