例題1
長さが\( 18cm\) の線香に火をつけて、その長さと時間の関係を調べたところ、火をつけてから \(8\) 分後に \(12cm\) になっていた。火をつけてから \(x\) 分後の線香の長さを \(ycm\) とします。次の問いに答えなさい。
(1) \(y\) を \(x\) の式で表しなさい。
(2) 線香の長さが \(10cm\) になるのは、火をつけてから何分後ですか。
(3) この線香は、火をつけてから何分後に燃えつきますか。
(4) \(x\) の変域と \(y\) の変域を求めなさい。
解説
線香は、規則正しく短くなっていきます。
一定の速さで短くなっていきます。
現実の線香の燃え方は、誤差もあるかもしれませんが、
数学の問題でこのように出題されたならば、もちろん
線香は一定の速さで短くなっていく
として解きます。
そうでないと問題として成立しませんしね。
暗黙の了解です。
さて、数学は目でみて解くのがいちばんわかりやすく、間違えにくく、
素早く処理ができます。
ですから、線香の長さが縮まっていく様子を、ささっとグラフに表してしましましょう。
もちろんラフな概形図でOKです。
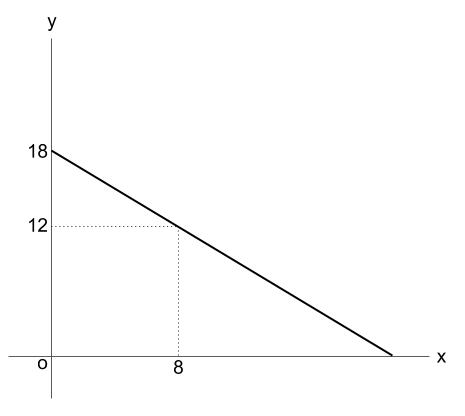
さて、グラフを利用してどんどん解いていきましょう。
(3)(4)はグラフを見れば一発で解けますね。
ここでは(1)から順に説明をしていきますが、
(3)(4)から先に解いたってもちろん構いません。
(1)\(y\) を \(x\) の式で表しなさい
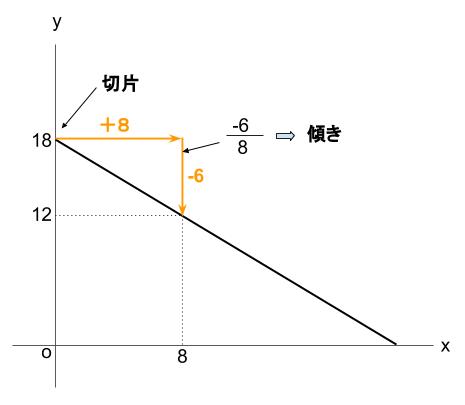
下図より、
傾きは \(-\displaystyle \frac{3}{4}\)
切片は、\(18\)
よって、求める直線の式は \(y=-\displaystyle \frac{3}{4}x+18\)
(2)線香の長さが \(10cm\) になるのは、火をつけてから何分後ですか
(1)で求めた式に、\(y=10\) を代入します。
\(10=-\displaystyle \frac{3}{4}x+18\)
これを解いて、\(x=\displaystyle \frac{32}{3}\)
よって、\(\displaystyle \frac{32}{3}\) 分後 です。
(3) この線香は、火をつけてから何分後に燃えつきますか
(1)で求めた式に、\(y=0\) を代入してもよいですし、グラフからも明らかです。
\(24\) 分後です。
(4) \(x\) の変域と \(y\) の変域を求めなさい
\(24\) 分後に燃え尽きるので、\(x\) の変域は、\(0 \leqq x \leqq 24\)
線香の長さは\(18cm\) から燃え尽きて \(0cm\) になるまでです。
\(y\) の変域は、\(0 \leqq y \leqq 18\)
スポンサーリンク
