例題1
下の表は長さ \(20mm\) のばねにおもりをつるし、おもりの重さとばねの長さの関係を調べたものである。おもりの重さを \(xg\),ばねの長さを \(ymm\) とします。次の問いに答えなさい。
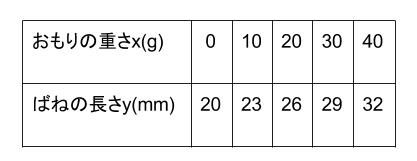
(1) おもりの重さが \(1g\) 増すごとに、ばねの長さは何\(mm\)ずつのびますか。
(2) \(y\) を \(x\) の式で表しなさい。
(3) \(24g\) のおもりをつるしたときの、ばねの長さを求めなさい。
解説
式処理だけで解いてもかまいませんが、ばねの長さが \(1\) 次関数になることを
積極的に利用して解くならば、グラフの活用です。
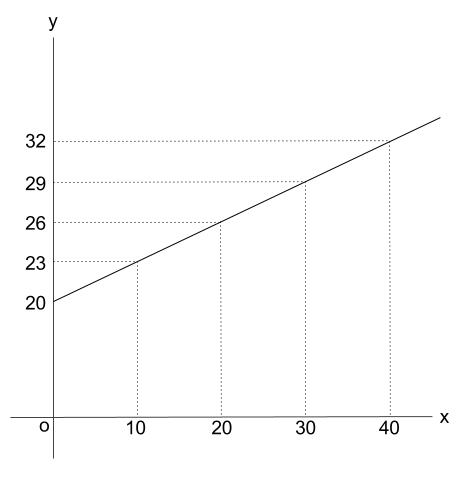
表をグラフにしてしまいましょう。
座標平面の右上部分のみを使ったグラフになります。
さっとラフにかけば十分です。
下図は \(y\) 軸の比率は不正確です。
ぜんぜんこれでOKです。概形がわかることが重要です。
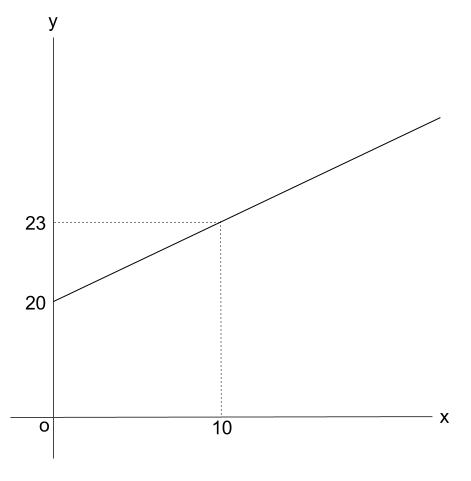
実はもっと簡略化した図でもかいません。
ばねは \(1\) 次関数!!ということを確かめたあとならば
(事実上暗記してしまいますね・・・)
下図くらいかけば十分でしょう。
さて解いていきましょう。
(1) おもりの重さが \(1g\) 増すごとに、ばねの長さは何\(mm\)ずつのびますか
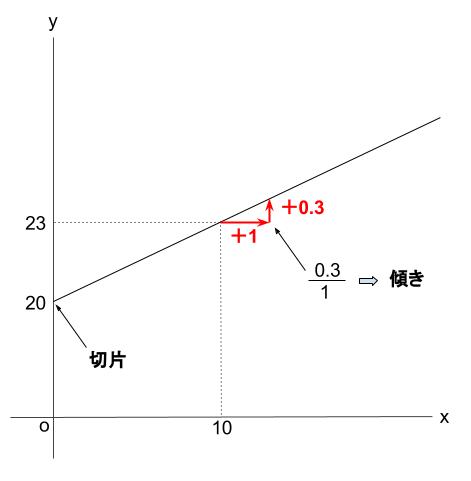
グラフから、\(10g\) 増えるごとに \(3mm\) ずつ伸びることがわかります。
よって、\(1g\) 増えるごとに、\(0.3mm\) ずつ伸びます。
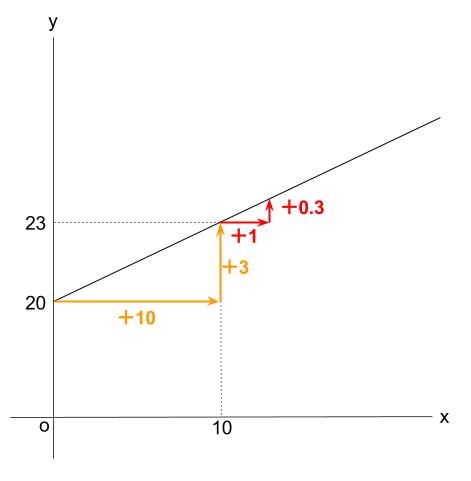
※グラフなしで、表からこの情報を得ることもできます。
(2)\(y\) を \(x\) の式で表しなさい
(1)で求めたものは、この直線の傾きですね!
よって、傾きが \(0.3\)、切片は \(20\) なので、求める式は、
\(y=0.3x+20\)
(3)\(24g\) のおもりをつるしたときの、ばねの長さを求めなさい
\(x=24\) を、(2)で求めた直線の式に代入します。
\(y=0.3×24+20\)
\(y=27.2\)
よって、ばねの長さは、\(27.2mm\) と求まります。
注 現実のばねはある一定以上の重さのおもりを吊り下げると、1次関数にように規則正しく伸びなくなります。ばねがのびきって縮まらなくなる、つまり壊れてしまうような重さのときです。数学において、これを考慮した出題はまずありえないでしょう。
スポンサーリンク
