1次関数のグラフ
比例をグラフで表現したように、もちろん \(1\) 次関数もグラフに表すことができます。
\(1\) 次関数のグラフの具体例をみて見ましょう。
\(y=2x+3\) のグラフは下図のようになります。
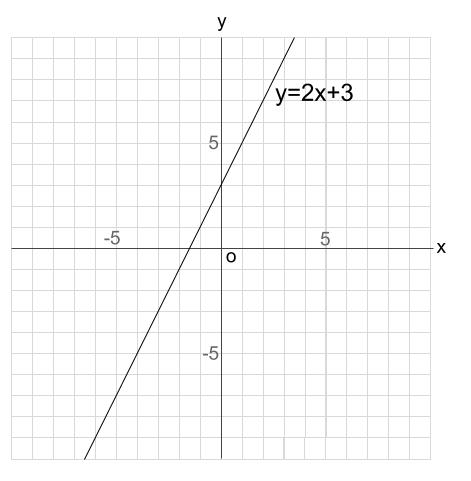
どうして、上のようなグラフになるのか確認しておきましょう。
グラフは、\(y=2x+3\) を満たす \(x\) 、\(y\) の点の集合です。
\(y=2x+3\) を満たす \(x\) 、\(y\) の組は無限にあります。
その \(1\) つ \(1\) つを座標平面上に点でとっていくと、直線になるのです。
これらを結ぶと上のグラフのようになるわけですね。
比例のときとまったく同じことです。
もちろんこの直線は、
\((0.1,3.2)\) や \((0.01,3.02)\) のような、点も通っています。
無限個の点の集合が、直線を作っているイメージです。
1次関数のグラフと比例のグラフ
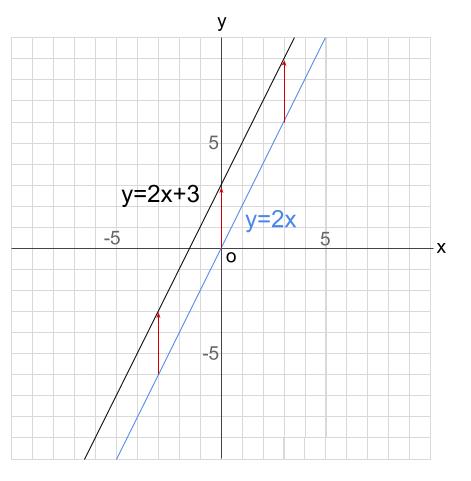
さて、\(y=2x+3\) という式が、上図のようなグラフになりました。
これは\(y=2x\) のグラフを \(y\) 軸方向に、\(+3\) 平行移動したものともいえます。
比例のグラフは、必ず直線になりましたね。
同様に、\(1\) 次関数のグラフも必ず直線になります。
比例のグラフをずらしただけですからね。
今後の学習の目安
みなさんが次に目指すことは
- 式を見て、グラフがかけること
- グラフをみて、それが表す式を導けること
の \(2\) つです。
比例のときとまったく同じことです。
順に学習していきましょう。
スポンサーリンク
