問題
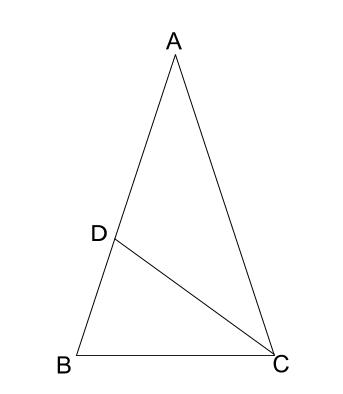
下の図の三角形 \(ABC\) において、点 \(D\) は辺 \(AB\) 上の点であり、
\(AB=AC\) 、\(AD=CD=CB=1cm\) である。辺 \(AB\) の長さを求めなさい。
解説
まずこの二等辺三角形の配置が有名配置であることを
知っておきたいです。
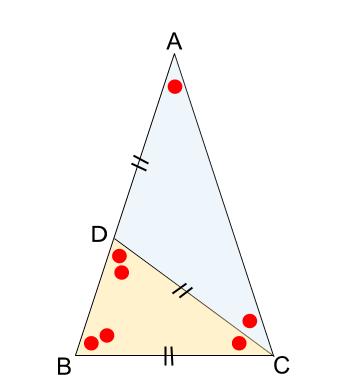
二等辺三角形 \(DCA\) の外角
と
二等辺三角形 \(CDB\) の内角より
角の大きさは下図のようになります。
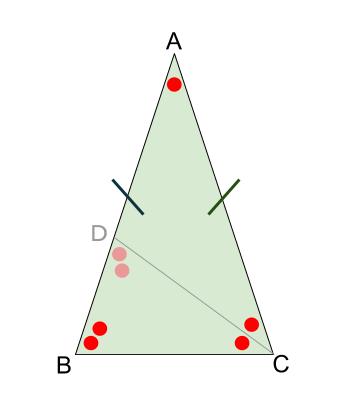
さらに、\(AB=AC\) という条件もあるので、
三角形 \(ABC\) は二等辺三角形です。
よって底角は、赤丸 \(2\) つ分ずつです。
以上より、
三角形 \(ABC\) と三角形 \(CDB\) は相似です。
ちなみに赤丸 \(1\) つの大きさも求まりますね。
\(36°\) です。
さて、いよいよこの問題を解く準備が整いました。
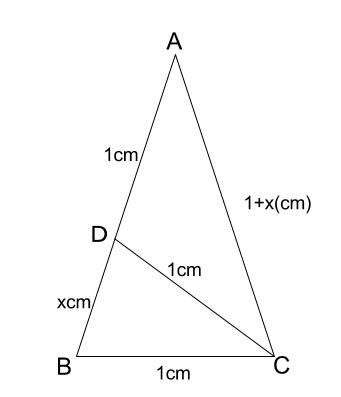
下図のように、\(DB=x(cm)\) とします。
ここで、相似な三角形に着目します。
三角形 \(ABC\) と三角形 \(CDB\) です。
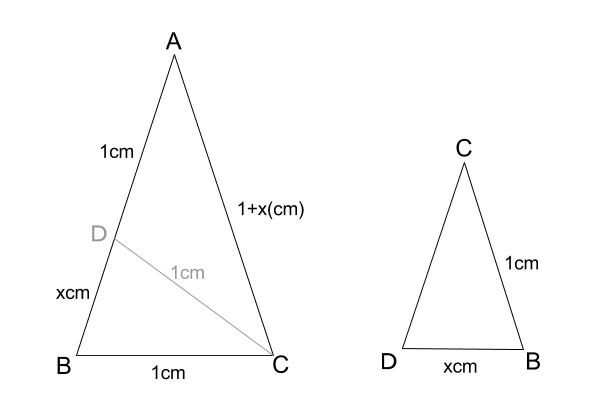
対応する辺の比が相似比です。
底辺に着目すれば相似比は
\(1:x\)
また、\(AC:CB\) は
\((1+x):1\)
これらは、どちらも同じ相似比なので等しい比です。
より、
\(1:x=(1+x):1\)
が成り立ちます。
内項の積と外項の積が等しいので、
\(x(1+x)=1\)
この \(2\) 次方程式を解きます。
\(x^2+x-1=0\)
\(x=\displaystyle \frac{-1 \pm \sqrt{1^2-4×1×(-1)}}{2×1}\)
\(x=\displaystyle \frac{-1 \pm \sqrt{5}}{2}\)
\(x\) は \(0\) より大きいので、
\(x=\displaystyle \frac{-1 + \sqrt{5}}{2}\)
求める長さは \(1+x\) なので
\(x+1=\displaystyle \frac{-1 + \sqrt{5}}{2}+1\)
\(=\displaystyle \frac{1 + \sqrt{5}}{2}\)
これが求める長さです。
スポンサーリンク
