問題
下の正方形の面積を \(1\) とするとき、面積が \(5\) の正方形を
定規とコンパスを用いて作図しなさい。

解説
\(1\) 辺が \(\sqrt{5}\) であればよいのですから、
\(\sqrt{5}\) の作図といえます。
このような長さの作図は、「三平方の定理」を活用します。
\(a^2+b^2=c^2\) のうち、本問は \(1\) と \(\sqrt{5}\) と何かになっています。
\(1\) が \(c\) のところにくることはないですから、
\(1^2+\sqrt{5}^2=c^2\) ・・・①
か
\(1^2+b^2=\sqrt{5}^2\) ・・・②
でしょう。
①ですと、 \(c=\sqrt{6}\) です。
\(\sqrt{6}\) という長さは簡単にはとれませんね。
②ですと、 \(b=2\) です。
これは簡単にとれます。
これで方針がたちました。
作図しましょう。
まず、正方形の \(1\) 辺を延長します。
そして、長さ \(2\) をコンパスを使って取ります。
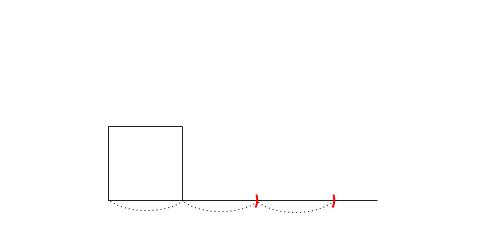
これで、 \(1:2:\sqrt{5}\) の直角三角形の完成です。
斜辺の長さが \(\sqrt{5}\) なので、この長さを用いて
正方形を作図します。
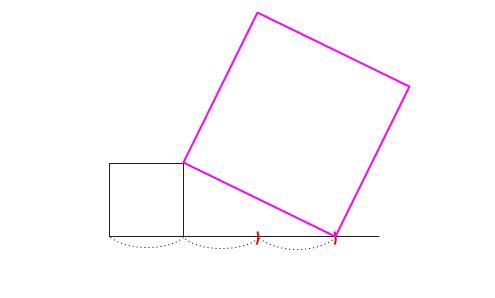
スポンサーリンク
