問題
下の図のように、円周上に 点 \(A,B,C,D\) があり、 \(AC\) と \(BD\) の交点を \(E\) とする。
次の問いに答えなさい。
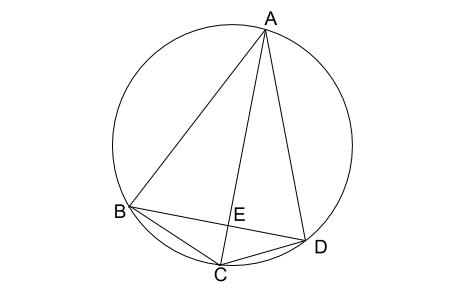
(1)\(\triangle ABE \backsim \triangle DCE\) となることを証明しなさい。
(2)\(AB=6\sqrt{5},CD=2\sqrt{5},BD=10cm,\angle AEB=90°\) のとき、 \(DE\) の長さを求めなさい。
解説
(1)\(\triangle ABE \backsim \triangle DCE\)
明らかに、「\(2\) つの角が等しい」から相似を示します。
円周角の定理より示せますね。
同じ色の丸は、円周角の定理より等しいことがいえます。
また、対頂角も等しいです。
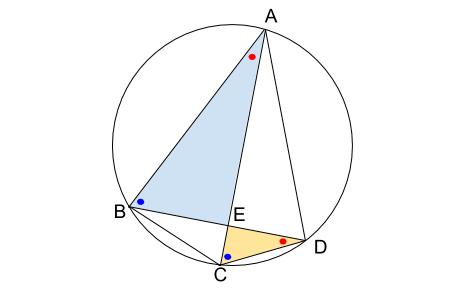
この証明は基本なので、省略します。
(2)\(DE\) の長さ
\(AB=6\sqrt{5}cm,CD=2\sqrt{5}cm,BD=10cm,\angle AEB=90°\) という与えられた情報を図にかきこみます。
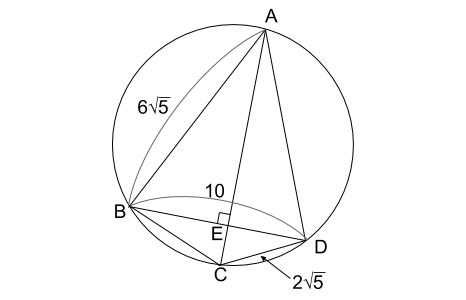
最終目標が \(DE\) の長さですから、
\(\triangle DCE\) を使うのでしょうし、
\(AB=6\sqrt{5}cm\) と与えられたからには、
\(\triangle ABE\) を使うのでしょう。
そしてこれは、(1)で相似であることを示した三角形ですから、
この \(2\) つが相似であることから解けそうです。
\(\triangle DCE\) を、\(\triangle ABE\) と同じ向きにぬき出して考えると
ミスが減りますし、考え易いです。
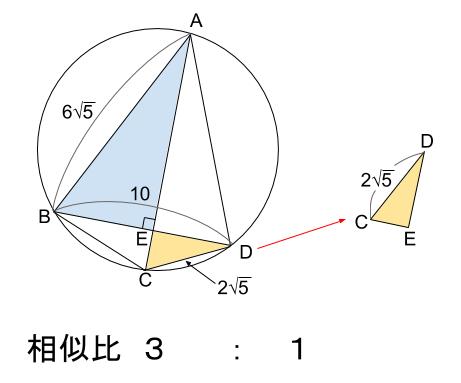
相似比が \(6\sqrt{5}:2\sqrt{5}=3:1\) とわかります。
ここで、求める長さである \(DE=x(cm)\) とおけば、
\(AE=3x\)
\(BE=10-x\) と表せます。
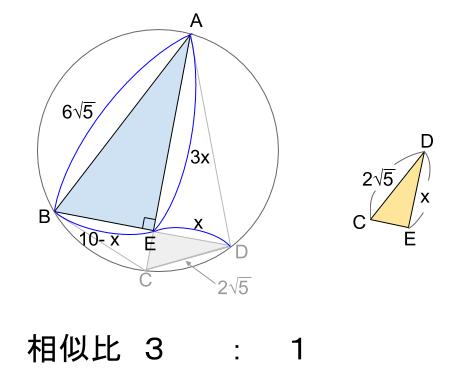
あとは、水色の三角形に三平方の定理を用いて
\((10-x)^2+(3x)^2=(6\sqrt{5})^2\)
あとは計算するのみです。
\(100-20x+x^2+9x^2=180\)
\(10x^2-20x-80=0\)
\(x^2-2x-8=0\)
\((x-4)(x+2)=0\)
\(x=-2,4\)
\(x\) は \(0\) より大きいので
求める \(DE\) の長さは \(4cm\) です。
スポンサーリンク
