問題
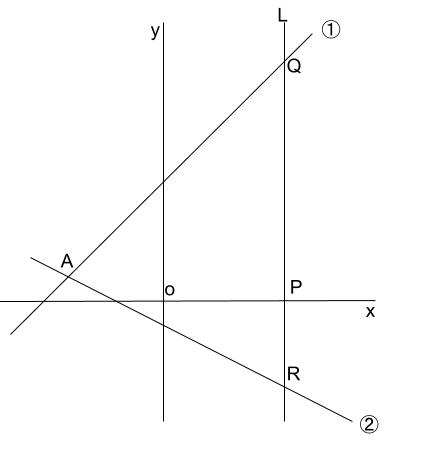
①は \(y=x+5\)、②は \(y=-\displaystyle \frac{1}{2}x-1\) のグラフであり、①と②の交点を \(A\) とする。また、 \(x\) 軸上に点 \(P\) をとり、点 \(P\) を通り \(y\) 軸と平行な直線 \(L\) をひきます。ただし、点 \(P\) の \(x\) 座標は正とします。
\(L\) と①の交点を \(Q\) 、\(L\) と②の交点を \(R\) とするとき、三角形 \(AQR\) の面積が \(75\) になる点 \(P\) の \(x\) 座標を求めなさい。
解説
求めるものを文字でおき、方程式をたてて解く。
これが中学数学の王道です。
この王道の解法をまずはマスターしましょう。
様々な問題で使える万能の解法です。
しかし・・・
それだけで満足しないでください。
「図形的性質を利用する別解」もあります。
とてもとても重要な解法です。
中学数学で、さらなる上を目指すときに立ちはだかる壁が、
この「図形」なのです。
関数の問題においても、座標平面上で図形の問題を解いているだけ、
という側面もあり、図形問題として処理できるかどうかが問われている難問も
存在します。
解法1 座標を文字でおく
\(P\) の \(x\) 座標を求めるのですから、
\(P\) の \(x\) 座標を文字でおく、
というのは自然な発想です。
\(P\) の \(x\) 座標を \(t\) としてみましょう。
すると、様々なものが \(t\) を用いて表せますね。
それらを、どんどん図にかきこんでいきます。
もちろん、点 \(A\) の座標も求めておきましょう。
①と②を連立して求めますね。 \(A(-4,1)\) です。
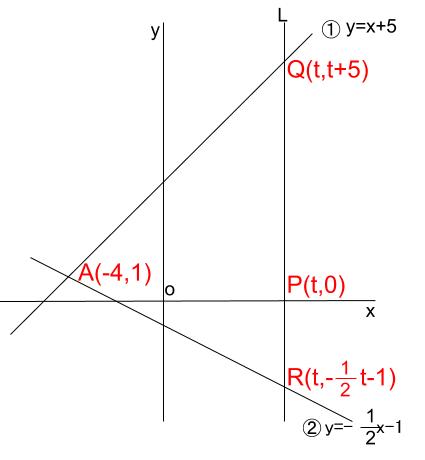
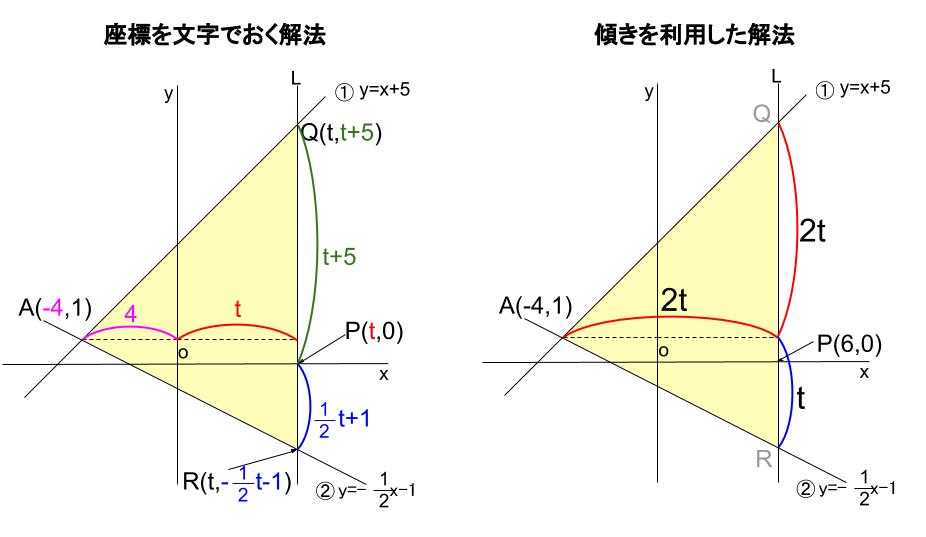
各点の座標から、三角形 \(AQR\) の辺の長さが分かります。
座標が負の値のときは気をつけましょう。
長さを表すためには、\(-1\) 倍して正の値にしましょう。
下図のピンクの線分と青い線分です。
符号に要注意ですよ!
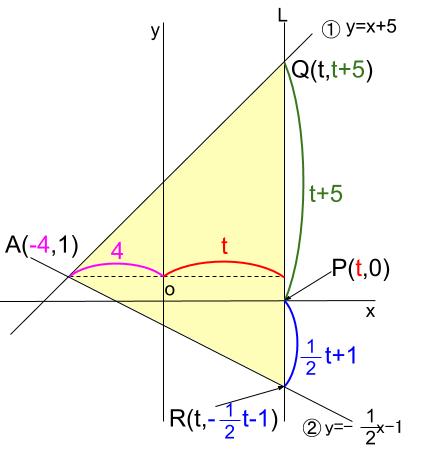
ここまでくれば、あとは計算あるのみです。
\(QR\) を底辺とすれば、その長さは
\((t+5)+(\displaystyle \frac{1}{2}t+1)=\displaystyle \frac{3}{2}t+6\)
※\(Q\) の \(y\) 座標から\(R\) の \(y\) 座標を引くことでも求められます。
高さは、ピンクと赤の線分の合計で、\(t+4\)
よって、三角形 \(AQR\) の面積が \(75\) になるとき以下の式が成り立ちます。
\((\displaystyle \frac{3}{2}t+6)×(t+4)×\displaystyle \frac{1}{2}=75\)
あとはこの \(2\) 次方程式を解きます。
両辺を \(2\) 倍して、左辺を展開すると、
\(\displaystyle \frac{3}{2}t^2+12t+24=150\)
両辺を \(3\) で割ると
\(\displaystyle \frac{1}{2}t^2+4t+8=50\)
両辺を \(2\) 倍して、右辺の \(50\) を左辺に移項すると
\(t^2+8t-84=0\)
因数分解して、
\((t-6)(t+14)=0\)
\(t=6,-14\)
点 \(P\) の \(x\) 座標は正なので、\(6\)
これで求まりました。
解法2 図形的性質の利用
上のような解法は、うまい解き方が見つからないときに威力を発揮します。
ガツガツと計算さえすれば、答えが求まるのです。
必ず身につけましょう。
しかし・・・
本問では、もっと「うまい解き方」があります。
座標平面と関数の情報を、図形的に活用するのです。
具体的には、「直線の傾き」です。
この情報を、図形的に利用しましょう。
\(直線の傾き=\displaystyle \frac{yの増加量}{xの増加量}\)
なので、
②の直線の傾き \(-\displaystyle \frac{1}{2}\)
①の直線の傾き \(1\) は、下図のようになっていることを示しています。
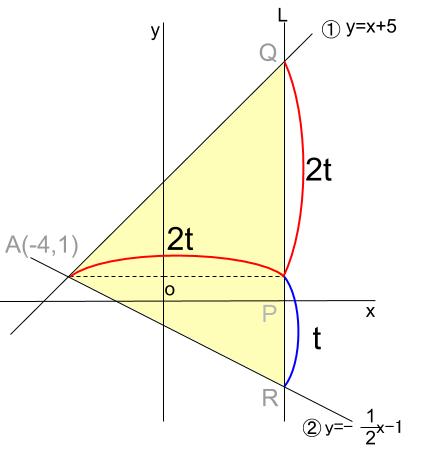
よって、上図のように \(t\) をおけば、
三角形 \(AQR\) の面積は、 \(3t×2t×\displaystyle \frac{1}{2}\) と表せます。
三角形 \(AQR\) の面積が \(75\) になるとき
\(3t×2t×\displaystyle \frac{1}{2}=75\)
\(t^2=25\)
\(t=\pm 5\)
\(t\) は \(0\) より大きいので
\(t=5\)
よって、下図のようになっていることがわかりました。
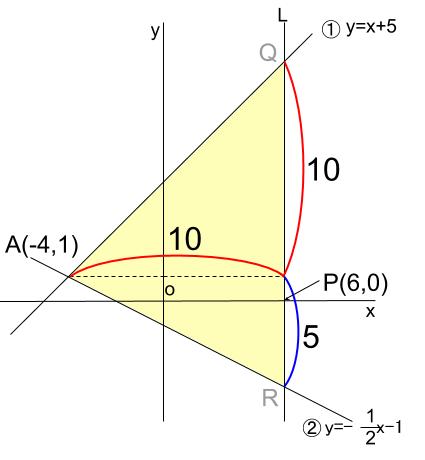
\(P\) は \(A\) より、\(10\) 正の方向にあるので、その \(x\) 座標は、
\(-4+10=6\)
これで求まりました。
なんと計算のスッキリしていることでしょう!!
この解法をみた後に、先ほどの、点 \(P\) の \(x\) 座標を \(t\) とおいた解法を
見てみてみれば・・・
三角形 \(AQR\) の長さを、不自然に細切れにしていることがわかります。
だから計算が面倒になってしまうのです。
参考:解法3 図形的性質の利用2
参考程度ですが、図形の利用としてもう \(1\) つ。
この問題は「ピラミッド型相似」になっているので、
それを利用できます。
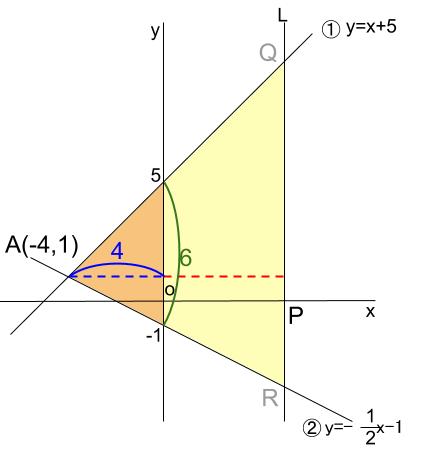
左のオレンジ色の三角形の面積は
①、②の\(y\) 切片や \(A\) の座標から求まります。
\(6×4×\displaystyle \frac{1}{2}=12\)
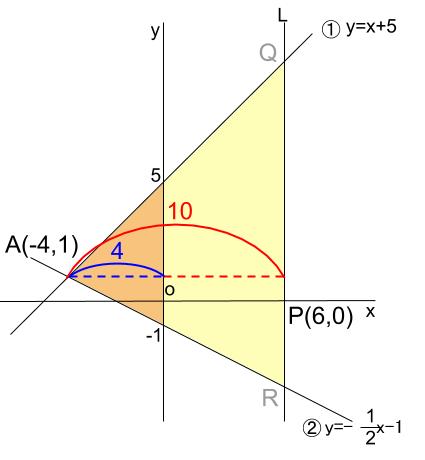
つまり、ピラミッド型相似で、面積比が \(12:75=4:25\)
になるときの \(P\) を求めたいのです。
相似な図形の面積比が \(4:25\) ならば、その相似比は \(2:5\) です。
\(4:25=2^2:5^2\) だからです。
よって、三角形 \(AQR\) の高さは \(4×\displaystyle \frac{5}{2}=10\)
となるので、\(P\)の \(x\) 座標は、
\(-4+10=6\)
これで求まりました。
スポンサーリンク
