分配の法則
「多項式と多項式の乗除」
いかついタイトルですが、難しく考えることはありません。
要は、「分配法則」です。
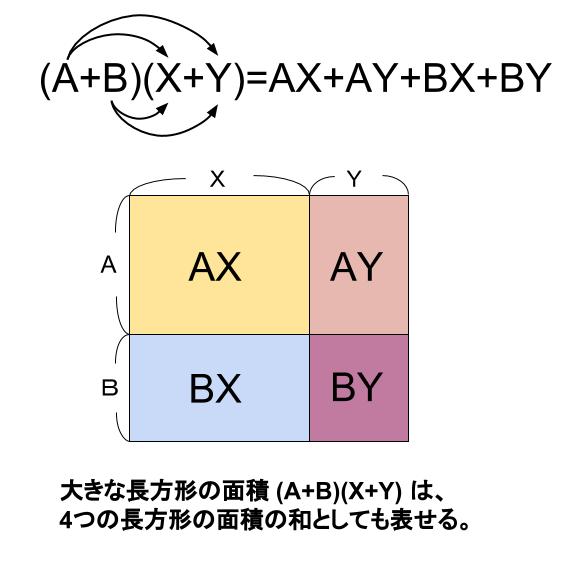
\((a+b)(x+y)=ax+ay+bx+by\)
順番にかけ算をしていくだけと覚えましょう。
このように、かっこをはずす計算をして、単項式の和の形に表すことを
「展開する」といいます。前回学習したことの再確認です。
もちろん
\((a+b)(x+y+z)=ax+ay+az+bx+by+bz\)
が成り立つたちます。
とにかく、順番にかけ算をしていくだけですね。
符号についての注意
負の数が入ってきたときの符号には要注意です。
\((a+b)(x-y)=ax-ay+bx-by\)
\((a-b)(x-y)=ax-ay-bx+by\)
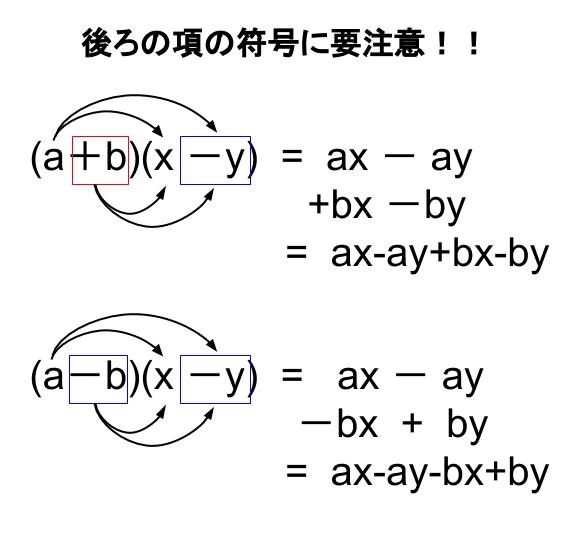
同類項を上手にまとめる
「多項式×多項式」の式の展開で最も多いのが、
\((x の1次式)×(x の1次式)\)
なのです。
具体例を見た方がいいですね。
例
次の式を展開しなさい。
\((2x-3)(x+1)\)
解説
もちろん順に計算していくだけなのですが、4つの単項式を横一列に並べるのではなくて
以下のようなかき方がおススメです!

\((2x-3)(x+1)=2x^2-x-3\)
例題
次の式を展開しなさい。
(1) \((x+2)(x+1)\)
(2) \((3x+2y)(2x-5y)\)
(3) \((x-3y)(4x-y)\)
(4) \((x-1)(x^2+x+1)\)
解答
(1) \((x+2)(x+1)\)
\(=x^2+3x+2\)
(2) \((3x+2y)(2x-5y)\)
\(=6x^2-15xy+4xy-10y^2\)
\(=6x^2-11xy-10y^2\)
(3) \((x-3y)(4x-y)\)
\(=4x^2-xy-12xy+3y^2\)
\(=4x^2-13xy+3y^2\)
(4) \((x-1)(x^2+x+1)\)
\(=x^3+x^2+x-x^2-x-1\)
\(=x^3-1\)
スポンサーリンク
