平均の速さとは
数学の文章題において速さを考えるとき、一定の速さで動くものばかりを扱ってきました。
太郎くんは分速 \(80m\) で進む、といえば、
減速することも加速することもなく常に分速 \(80m\) で進む太郎くんを考えたわけです。
現実の世界ではどうでしょう。
新幹線が東京~大阪の約 \(500km\) を約 \(2\) 時間で進むとき
時速 \(250km\) で進んだのでしょうか?
新幹線は時速 \(0km\) から徐々に加速し、
最高到達時速は \(300km\)、
そして名古屋で止まるために減速をしたり・・・
刻一刻と速さは変化しています。
この新幹線が時速 \(250km\) であるというのは、
「平均の速さ」のことなのです。
平均の速さとは、
\(移動距離 ÷ 移動した時間\)
のことです。
もしも、
移動中の速さが、常に一定だったならば・・・
最初から最後まで、ずっと同じ速さだったならば・・・
これが平均の速さなのです。
重力にひかれて加速される物体の速さ
中学生において、平均の速さは 「\(2\) 乗に比例」の学習時に学びます。
物体が重力にひかれて落下してくとき、物体の速さは刻一刻と加速されていきます。
常に一定の速さで動かない物を考えるはじめての機会なのです。
物体が重力にひかれて落下してくとき、
移動した時間 \(x\) と移動距離 \(y\) の関係が、\(2\) 次関数になることが知られています。
※過去の科学者が実験を繰り返すことで突き止めました。
このような速さは、「距離÷時間」で求めることができないため、「平均の速さ」を求めることにします。
例題で学習しましょう。
※高校生になると、この速さを求める画期的な方法、「微分」を学習します。
例題1
ボールがある坂道を転がり始めてから \(x\) 秒間で転がる距離を \(ym\) とするとき、\(y\) は \(x\) の \(2\) 乗に比例します。最初の \(2\) 秒間に転がる距離が \(8m\) のとき、次の問いに答えなさい。
① \(y\) を \(x\) の式で表しなさい。
② ボールが転がりはじめてから \(3\) 秒間で、何 \(m\) 転がりますか。
③ \(3\) 秒後から \(5\) 秒後までの平均の速さを求めなさい。
④ \(a\) 秒後から \(a+2\) 秒後までの平均の速さが秒速 \(10m\) のとき、\(a\) の値を求めなさい。
解説
\(y\) は \(x\) の \(2\) 乗に比例するとあるので、\(y=ax^2\) とします。
① \(y\) を \(x\) の式で表しなさい。
\(x=2\) のとき、\(y=8\) なので、これを \(y=ax^2\) に代入すると
\(8=a×2^2\)
\(a=2\)
よって、求める式は
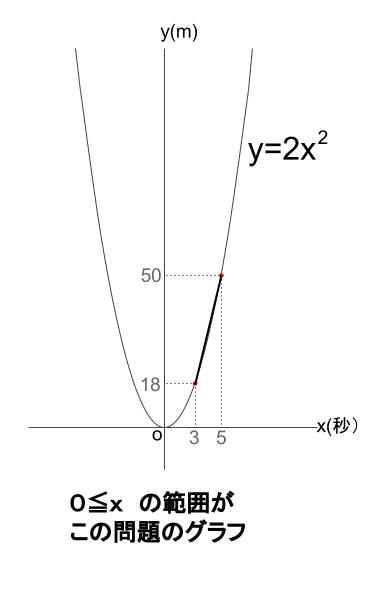
\(y=2x^2\)
② ボールが転がりはじめてから \(3\) 秒間で、何m転がっているか
①で求めた式に、\(x=3\) を代入します。
\(y=2×3^2\)
\(y=18\)
より、\(18m\) です。
③ \(3\) 秒後から \(5\) 秒後までの平均の速さを求めなさい。
\(5\) 秒後までに何 \(m\) 転がったか計算します。
\(y=2×5^2\)
\(y=50\)
より、\(50m\) です。
つまり、
\(3\) 秒後に \(18m\)
\(5\) 秒後に \(50m\)
この \(3\) 秒後から \(5\) 秒後までの \(2\) 秒間で、 \(50-18=32m\) 進んでいます。
よって、この間の平均の速さは
\(32÷2=16\)
より、秒速 \(16m\) です。
別解
平均の速さが、この関数のグラフにおける変化の割合と同じであるとわかれば、
変化の割合の公式一発です。
\(平均の速さ=変化の割合=2(3+5)=16\)
よって、秒速 \(16m\) です。
\(a\) 秒後から \(a+2\) 秒後までの平均の速さが、秒速 \(10m\) のとき、\(a\) の値を求めなさい。
平均の速さは、③で見た通り「変化の割合」と一致します。
よって、変化の割合の公式を使うのが速いですね。
\(平均の速さ=変化の割合=10=2(a+a+2)\)
なので
\(10=4a+4\)
\(a=1.5\)
以上、求まりました。
参考・自由落下
坂道を転がすのではなく、空中で物を落とした時、物が(地球の)重力に引かれて落ちていくことを
「自由落下」といいます。
※厳密には空気抵抗などをまったく考慮しないときです。
地球で、この自由落下をするとき、
物が落ち始めてから \(x\) 秒後に落下した距離を \(ym\) とすると、
\(y=4.9x^2\)
となります。
比例定数の \(4.9\) は実験から観測された値で、およその値です。
\(1\) 秒後には \(4.9m\) 落下
\(2\) 秒後には \(19.6m\) 落下
\(3\) 秒後には \(44.1m\) 落下
\(4\) 秒後には \(78.4m\) 落下
と計算されます。
どんどん加速していくため、
たった\(4\) 秒で \(78.4m\) も落下するんですね!
\(3\) 秒から \(4\) 秒までの \(1\) 秒間で、 \(34.3m\) 進むため
その平均の速さは、秒速 \(34.3m\) であり、
時速にすると、時速 \(123.48km\) です。
たった \(4\) 秒で!!
びっくりですね。
実際は空気抵抗があるため、もう少し遅く、スカイダイビングでも最終的には時速 \(200km\) 程度で加速が止まるそうです。
よりくわしく学習したい人は、高校生の物理でやりますので、お楽しみに。
スポンサーリンク
