基本用語の確認
円 \(O\) の \(\stackrel{ \Large \frown }{ AB }\) に対して、\(\angle AOB\) を、\(\stackrel{ \Large \frown }{ AB }\) に対する中心角という。
円 \(O\) の \(\stackrel{ \Large \frown }{ AB }\) に対して、 \(\stackrel{ \Large \frown }{ AB }\) を除いた円周上に点 \(P\) をとる。
\(\angle APB\) を、\(\stackrel{ \Large \frown }{ AB }\) に対する円周角という。
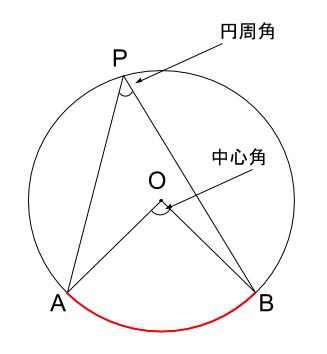
円周角の定理
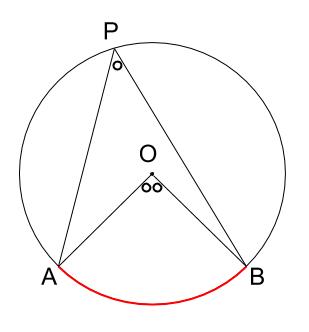
円周角は中心角の半分
\(\stackrel{ \Large \frown }{ AB }\) に対する円周角の大きさは、\(\stackrel{ \Large \frown }{ AB }\) に対する中心角の大きさの半分である。
※円周角は中心角の半分!と覚えましょう。
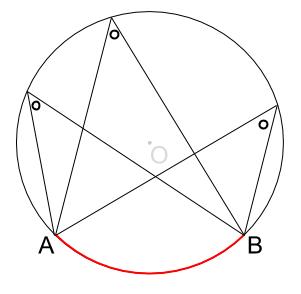
同じ弧に対する円周角は等しい
下図のように、\(\stackrel{ \Large \frown }{ AB }\) に対する円周角は無数にありますが、すべて角の大きさは同じになります。
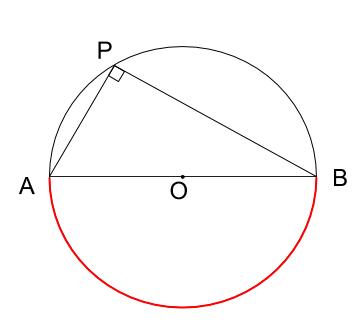
半円の弧に対する円周角は90°である。
上記 \(2\) つから導かれることですが、中心角が \(180°\) のときは、特別に大事な図形として覚えておきましょう。
円周角が直角になります。
半円⇒\(90°\) という暗記も大事なのですが、
直径⇒\(90°\) という暗記もしておきましょう。
円周角の大きさは弧の長さに比例する
これも上の基本事項から導かれます。
弧の長さが \(2\) 倍になれば、円周角も \(2\) 倍になります。
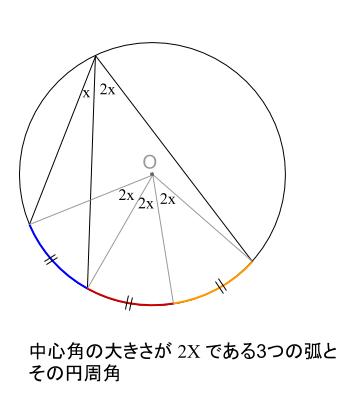
上の図で、
弧の長さが \(2\) 倍、\(3\) 倍になれば、円周角が \(2\) 倍、\(3\) 倍になることが確かめられます。
