例題7
下の図の角 \(x\) の大きさを求めなさい。
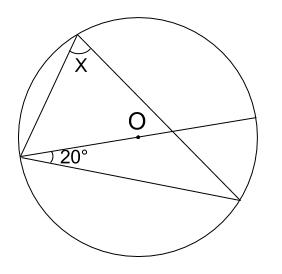
解説
赤い点線を引いたところ、この円周角は \(20°\) です。
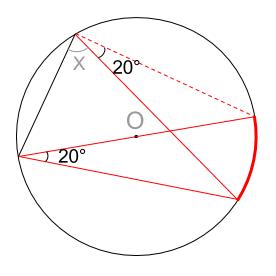
次に、半円の弧に対する円周角は \(90°\) なので、
\(x=90-20=70°\)
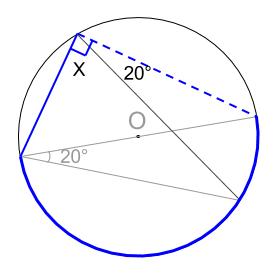
そもそもどうしてこのような解き方を思いつくのか、
というと、注目すべき角、弧が下図のようになっているからです。
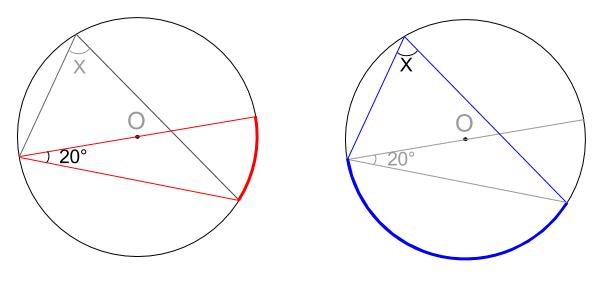
\(2\) つの弧を合わせると、半円の弧になることから、上のような解法になります。
また、上の解法は \(20°\) を別の箇所につくる解法でしたが、別にそのようなことをしなくても構いません。
\(2\) つの弧を合わせると、半円の弧になるから、\(x=90-20=70°\)
という解き方でも構いません。
例題8
下の図の角 \(x\) の大きさを求めなさい。
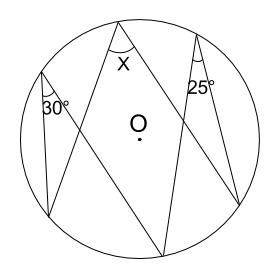
解説
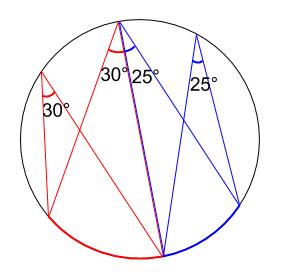
同じ弧の円周角は等しいので、下図のようになります。
\(x=30+25=55°\)
例題9
下の図の角 \(x\) の大きさを求めなさい。
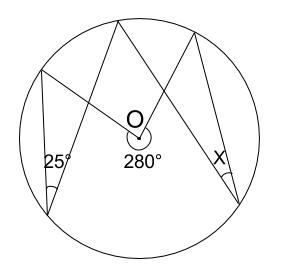
解説
同じ弧に対する中心角は、円周角の \(2\) 倍の大きさなので、下図のようになります。
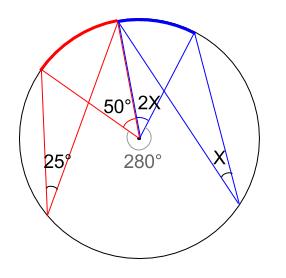
\(360-280=50+2x\)
より、\(x=15°\) と求まります。
