円の基本的な性質
弦、接線、接点という言葉は覚えていますか?
その図形的性質は覚えていますか?
覚えていないとまったく問題が解けませんので、必ず暗記しましょう。
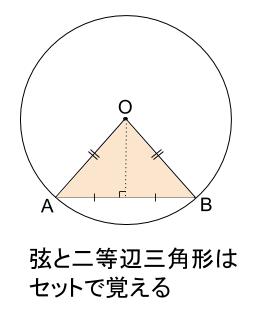
弦と二等辺三角形
円 \(O\) との弦 \(AB\) があれば、三角形 \(OAB\) が二等辺三角形になる。
二等辺三角形の図形的性質は大丈夫ですね?
左右対称です。
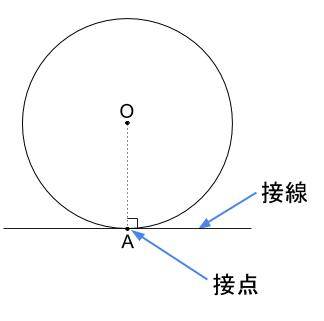
接線と半径は垂直
半径(正しくは円の中心と接点を結んだ線分)と、その点における接線は垂直
例題1
半径が \(11cm\) の円 \(O\) で、中心との距離が \(5cm\) である弦 \(AB\) の長さを求めなさい。
解答
このように、図が与えられないで出題されることもあります。
このようなときは、ささっと図をかきましょう。
あまりていねいな図である必要はありません。
「中心と弦との距離が \(5cm\) という情報を図示できますか?
点と直線(線分)の距離とは、
「点から直線に引いた垂線の長さ」
のことです。
これだって暗記です。
暗記ゼロでは数学の学習はできませんよ。
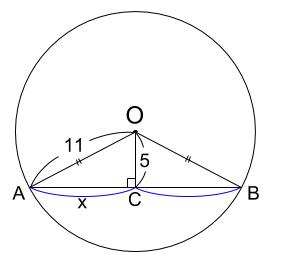
図示ができれば簡単です。
三角形 \(OAC\) に三平方の定理を用いて
\(11^2=x^2+5^2\)
\(121=x^2+25\)
\(x^2=96\)
\(x=±\sqrt{96}\)
\(=±4\sqrt{6}\)
\(x\) の値は明らかに正なので、
\(x=4\sqrt{6}\)
これで答えにしてはいけませんね。
求める長さは、\(x\) ではなくて、\(2x\) なので
\(2x=8\sqrt{6}\)
弦 \(AB\) の長さは、\(8\sqrt{6}cm\)
例題2
円 \(O\) の中心と点 \(A\) との距離が \(16cm\) であり、点 \(A\) から円 \(O\) 上の点 \(P\) に接線を引いたとき \(AP\) の長さが \(12cm\) であった。円 \(O\) の半径の長さを求めなさい。
解答
図が与えられていないので図示するところからはじめます。
円 \(O\) の半径の長さが不明なので、正確な図は絶対にかけません。
概形がわかればよいのです。
円外の点から円に接線を引くとき、左右対称な \(2\) 本の接線が引けます。
どちらで解いても関係ないですね。
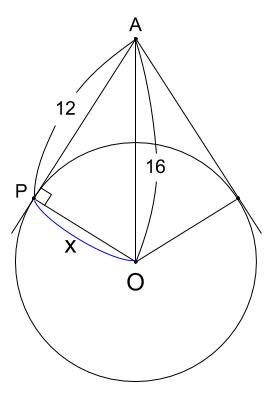
求める半径の長さを \(x\) とすると
三平方の定理より
\(x^2+12^2=16^2\)
\(x^2+144=256\)
\(x^2=112\)
\(x=±\sqrt{112}\)
\(=±4\sqrt{7}\)
\(x\) の値は明らかに正なので、
\(x=4\sqrt{7}\)
よって、円 \(O\) の半径の長さは、\(4\sqrt{7}cm\)
