三平方の定理の証明
三平方の定理はなぜ成立するのか。
ありとあらゆる直角三角形に成り立つというのです。不思議な気がしませんか?
実に様々な証明がありますが、
中学生が学習しておくべき最も重要な証明を紹介します。
三平方の定理 証明の例
下図のような直角三角形を \(4\) つをぐるりと並べて、\(1\) 辺の長さが \(a+b\) の正方形を作ります。
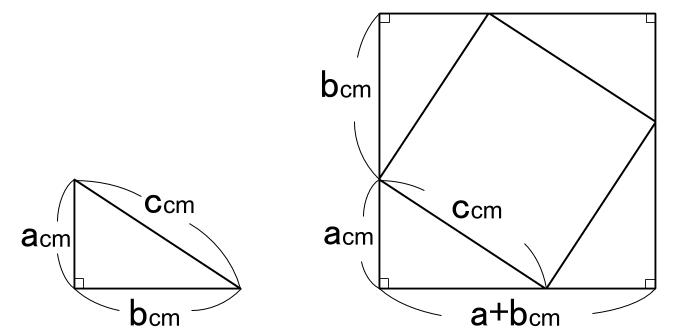
この図形の面積を \(2\) 通りに考えます。
1辺が \(a+b\) の正方形の面積
1辺が \(a+b\) の正方形の面積はもちろん、\((a+b)^2=a^2+2ab+b^2\)
求まりました。
では次に別の求め方で求めます。
三角形4つと中の四角形の和
三角形 \(1\) つの面積は、\(\displaystyle \frac{1}{2}ab\)
中の四角形の面積は、\(c^2\)
よって全体の面積は、\(\displaystyle \frac{1}{2}ab×4+c^2=2ab+c^2\)

ところで、中の四角形の面積は、\(c^2\) としましたが、
これは中の四角形が正方形であるということで話を進めました。
本当に正方形なのでしょうか?
論理的に説明できますか?
\(4\) 辺が等しいだけでは、ひし形であることまでしか言えませんよ。
\(1\) つの角が直角であることを示しましょう。
下図の ◎ の角の大きさが直角であることを示すことが目標です。
左下の直角三角形の内角の和より、●と▲の和は \(90°\) です。
次に ◎ の角のある一直線\(=180°\) より、
●+▲+◎\(=180°\)
よって、◎\(=90°\)
これで示せました。

2通りで得られた面積は等しい
別々の方法で面積を求めましたが、これらは互いに等しいので
\(2ab+c^2=a^2+2ab+b^2\)
両辺から\(2ab\)を引けば、
\(c^2=a^2+b^2\)
これで三平方の定理が得られました!!!
三平方の定理の驚異的証明
上の証明は、中学数学の重要事項である「展開」と「相似」を用いており、使用する図形もわかりやすいもので、とても覚えやすいものです。
必ず、理解・暗記して欲しい、学習効果の高い証明です。
しかし・・・
直角三角形を \(4\) つぐるりと並べるなんて、かなり人工的な、作為的な証明だなあという印象は否めません。
こんな証明、いったい誰がどうやって思いついたのでしょうね。
また、三平方の定理の証明は、百通り以上の異なる証明が発表されていますが、いずれも人工的な、作為的な印象のするものばかりです。
これらはつまり、「定理の結果を知った上で、後から考えられた証明」なのでしょう。
そこで、三平方の定理の証明で、極めてシンプルで美しいものを紹介します。
この証明も中学数学のエッセンスの詰まったものになります。
おそらく三平方の定理の証明として、もっとも簡潔で美しいものなのではないでしょうか。
もっとも簡潔で美しい証明
下の三角形において、\(3\) つの直角三角形は相似です。
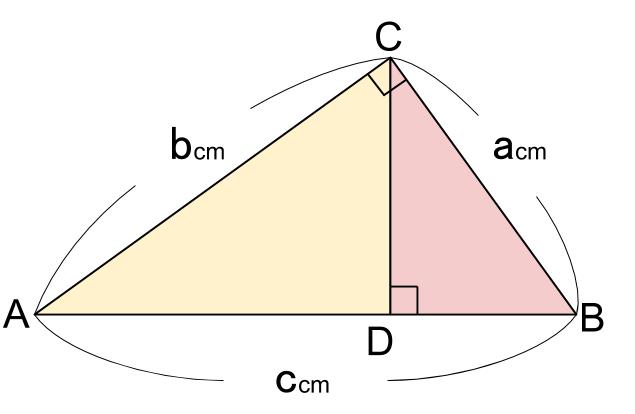
大三角形 \(ABC\) の斜辺は \(ccm\)
中三角形 \(ACD\) の斜辺は \(bcm\)
小三角形 \(BCD\) の斜辺は \(acm\)
なので、相似比は、\(c:b:a\) です。
よって、面積比は、\(c^2:b^2:a^2\) です。

大三角形 \(ABC\) の面積は、中三角形 \(ACD\) と小三角形 \(BCD\) の面積の和なので、
\(c^2=b^2+a^2\)
よって、三平方の定理が証明できました。
なんと簡潔な証明でしょう!!
どの証明が簡潔なのか、美しいのかは、主観なので数学的に決定できるものではありませんが、おそらくこの証明がナンバー1でしょう。
そもそもこれこそが三平方の定理の人類史上初の証明なのではないでしょうか?
いや、正しくはわかりませんけど。
