二等辺三角形
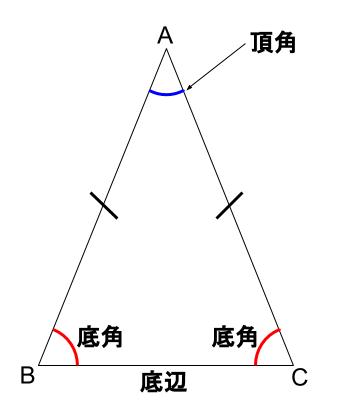
\(2\) つの辺が等しい三角形を二等辺三角形といいます。
また等しい辺との位置に応じて、頂角、底角、底辺という名前がつきます。
重要な性質
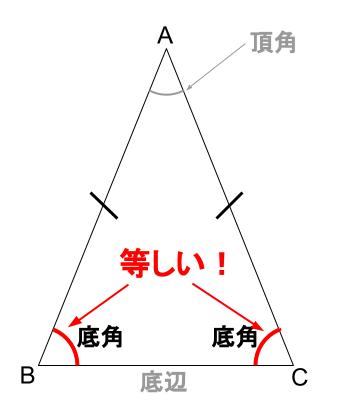
二等辺三角形の底角は等しい
下図で、\(\angle ABC=\angle ACB\)
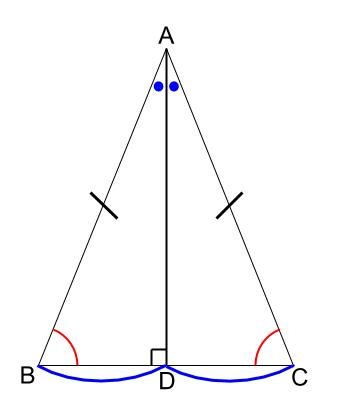
二等辺三角形の頂角の二等分線は、底辺を垂直に2等分する
下図で、\(BD=CD\)
これは、二等辺三角形が線対称な図形であるということと同じ意味です。
※頂角の二等分線を対称の軸として線対称
例題1
下の図で、\(AB=AC\) です。 \(\angle x,y\) の大きさを求めなさい。
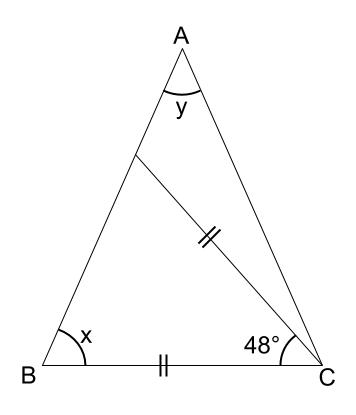
解説
下図の水色の三角形が、二等辺三角形なので、
\(\angle x=(180-48)÷2=66°\)

続いて \(y\) は、二等辺三角形 \(ABC\) の底角が \(66°\) であることから、
\(\angle y=180-66×2=48°\)
と求まります。
水色の三角形と三角形 \(ABC\) は、\(3\) つの角がそれぞれ同じ大きさなんですね!
※ちなみにこれを「相似」といいます。中学 \(3\) 年生で習います。
例題2
下の図で、 \(\angle x\) の大きさを求めなさい。
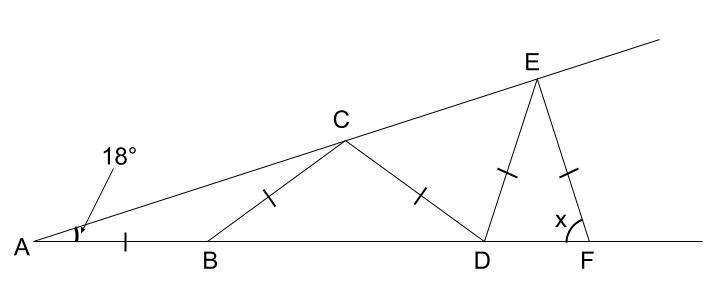
解説
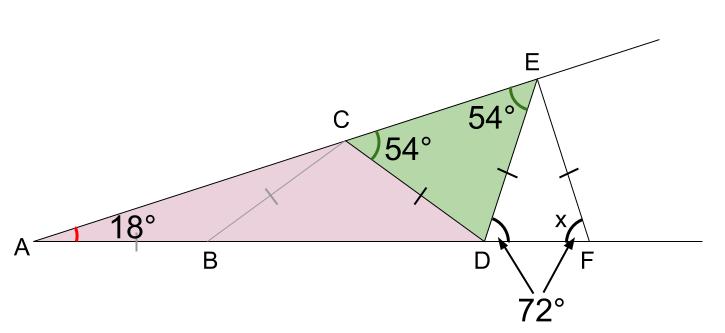
三角形 \(BCA\) は二等辺三角形なので底角が等しい。
また三角形の外角の性質より、\(\angle CBD=18+18=36°\)
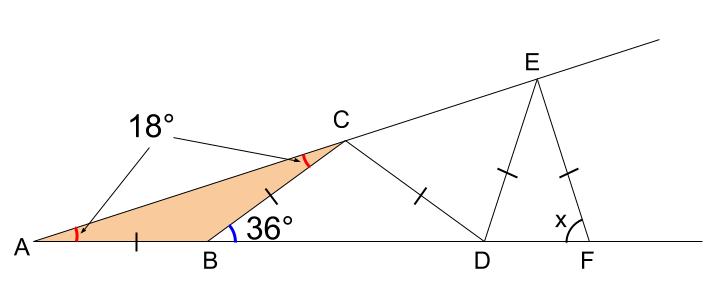
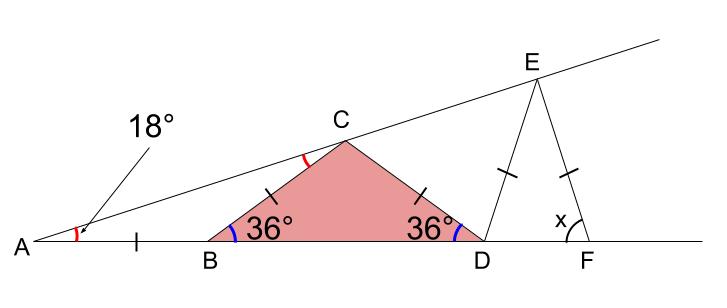
三角形 \(CBD\) は二等辺三角形なので底角が等しい。
また三角形 \(CAD\) の外角の性質より、\(\angle DCE=18+36=54°\)
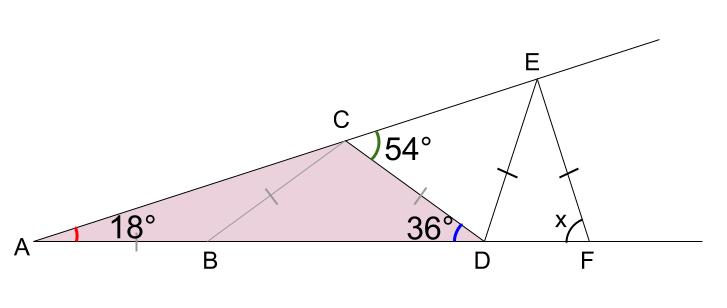
同様に、
三角形 \(DEC\) は二等辺三角形なので底角が等しい。
また三角形 \(EAD\) の外角の性質より、\(\angle EDF=18+54=72°\)
また三角形 \(EDF\) は二等辺三角形なので底角が等しいので
\(\angle x=72°\)
スポンサーリンク
