対頂角
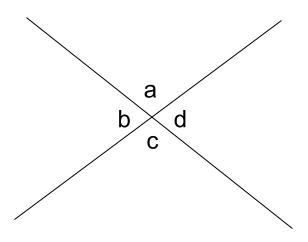
\(\angle a\) と \(\angle c\) のように、向かい合った \(2\) つの角を対頂角といいます。
対頂角は必ず等しいので
\(\angle a=\angle c\)
\(\angle b=\angle d\)
例題
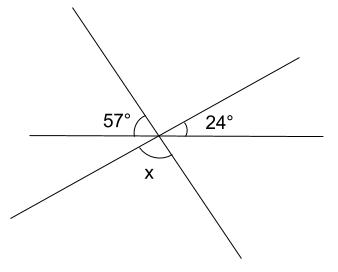
下の図で、\(\angle x\) の大きさを求めなさい。
解答
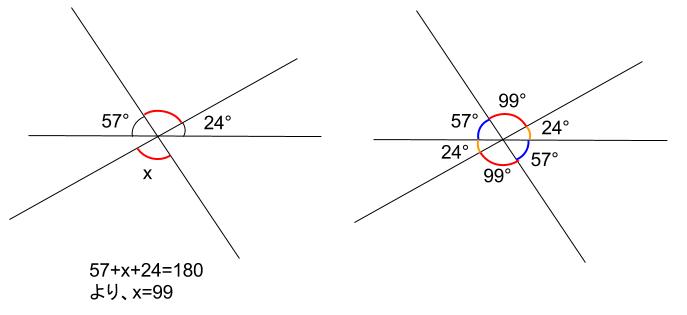
対頂角(向かい合う角)は等しいので、下図のようになります。
\(\angle x=99°\) です。
同位角と錯角
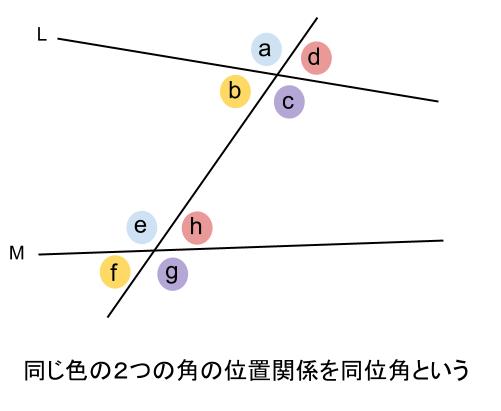
下の図で、\(\angle a\) と \(\angle e\) のような位置にある \(2\) つの角を同位角といいます。
同じ色の角が同位角です。
つまり、
\(\angle b\) と\(\angle f\) は同位角
\(\angle c\) と\(\angle g\) は同位角
\(\angle d\) と\(\angle h\) は同位角
また、\(\angle b\) と \(\angle h\) の \(\angle c\) と \(\angle e\) のような位置にある \(2\) つの角を錯角といいます。
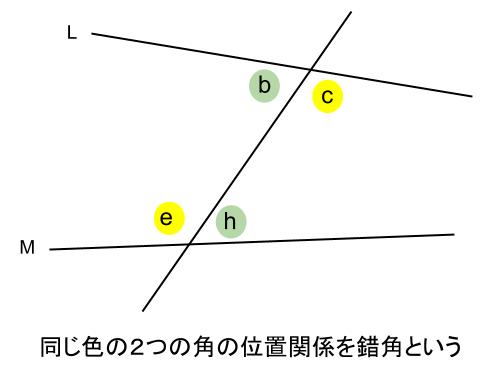
平行線の同位角と平行線の錯角
下図のように、直線 \(L\) と直線 \(M\) が平行のとき、同じ記号の角の大きさは等しくなります。
平行線の同位角は等しい
平行線の錯角は等しい
この \(2\) つが成り立ちます。
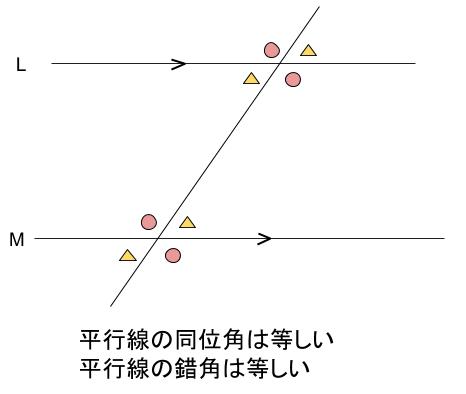
同位角と錯角は、平行線のときにしか注目しないと言っていいくらいです。
例題
下の図で、\(\angle x\) の大きさを求めなさい。
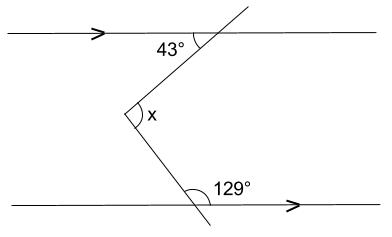
解答
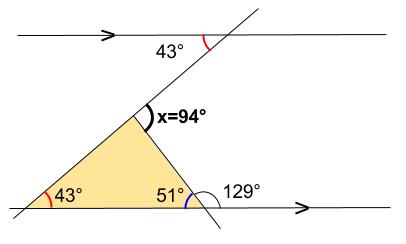
平行線をもう \(1\) 本、補助線として引きます。
青い角度は、\(180-129=51\)
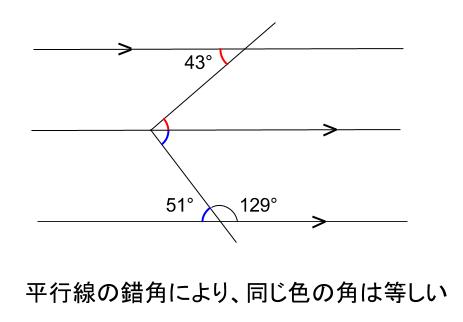
よって
\(\angle x=43+51=94\)
別解
下図のように線を延長する補助線を引くことで、平行線の錯角が利用できます。
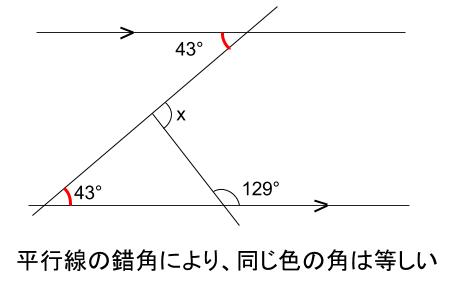
三角形の外角により、
\(\angle x=43+51=94\)
スポンサーリンク
