例題1
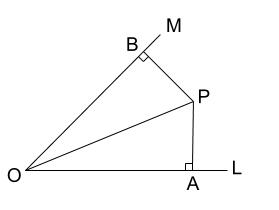
下の図のように、点\(P\) から直線 \(L,M\) にそれぞれ垂線 \(PA,PB\) をひく。
このとき、\(PA=PB\) ならば、\(OP\) は \(\angle BOA\) の二等分線であることを証明しなさい。
解説
中学 \(1\) 年の作図で、角の二等分を学習しました。
このとき、「\(2\) 辺から等しい距離にある直線は角の二等分線」
ということを暗記したはずです。
暗記したはずのことですが、改めて証明せよというのです。
普通に問題を解くときは、証明なしで使っていい事実ですが、
改めて証明せよ、と言われれば証明しなくてはなりません。
証明の方針
\(\triangle POA \equiv \triangle POB\)
を示せばよいことはすぐにわかりますね?
この \(2\) つは直角三角形です。
斜辺ともう \(1\) つ(辺か角)がそれぞれ等しければいいのです。
明らかに斜辺は \(PO\) で共通。
仮定より \(AP=BP\) です。
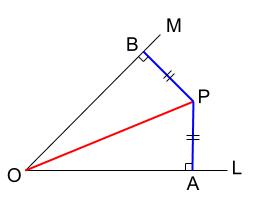
斜辺と他の \(1\) 辺がそれぞれ等しいので \(\triangle POA \equiv \triangle POB\) です。
解答
\(\triangle POA\) と \(\triangle POB\) において
仮定より、\(AP=BP\) ・・・①
\(PO\) は共通・・・②
①、②より、
直角三角形の斜辺と他の \(1\) 辺が等しいので
\(\triangle POA \equiv \triangle POB\)
合同な図形の対応する角は等しいので、
\(\angle POA=\angle POB\)
よって、\(OP\) は \(\angle BOA\) の二等分線である。
例題2
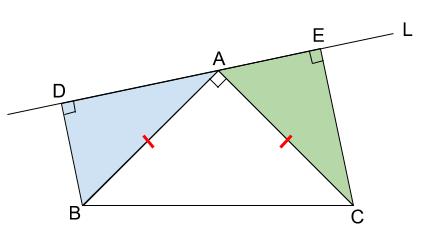
直角二等辺三角形 \(ABC\) の頂点 \(A\) を通る直線 \(L\) に、頂点 \(B,C\) からそれぞれ垂線 \(BD,CE\) をひいた。このとき、\(\triangle ABD \equiv \triangle CAE\) を証明しなさい。

解説
有名図形配置です。
証明はやや独特の手法を用います。
きちんと理解した上で、暗記もしてください。
中学3年生で学習する「三平方の定理」をこの図形配置で証明することが非常に多く、
また様々な問題の種になり得る図形配置です。
解答
\(\triangle ABD\) と \(\triangle CAE\) の斜辺が等しいことは仮定より
与えられています。
よって、「あと \(1\) つの辺が等しい」か「あと \(1\) つの角が等しい」
のいずれかが言えればよいことになります。
どちらが言えそうか考えてみてください。
なかなか難しいですね。
ここがやや独特の手法を用いる箇所です。
言えるのは、
「あと \(1\) つの角が等しい」
になります。
下図の \(5\) つの赤い角に注目します。
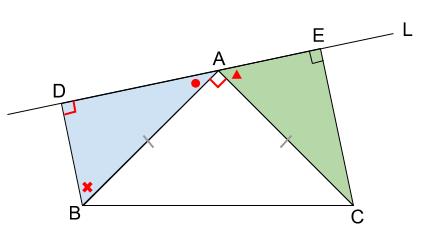
点 \(A\) に集まった \(3\) つの角の和は一直線なので \(180°\) です。
\(○+△+90°=180°\)・・・①
また左の青い三角形の内角の和は \(180°\) です。
\(○+×+90°=180°\)・・・②
①、②より、
\(△=×\) がいえます!
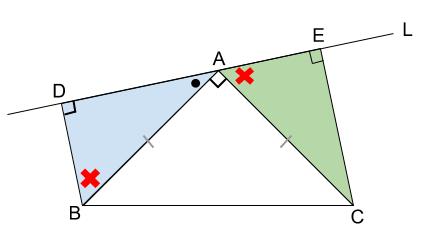
これで、斜辺と他の \(1\) つの鋭角がそれぞれ等しいので合同と言えます。
※もちろん右の緑の三角形を用いて同様の説明が可能です。
解答
\(\triangle ABD\) と \(\triangle CAE\) において
仮定より、\(\triangle ABC\) が二等辺三角形なので、\(AB=CA\) ・・・①
仮定より、\(\angle BDA=\angle CAB =90°\) ・・・②
三角形の内角の和は \(180°\) なので②より、
\(\angle ABD=180°-\angle BDA-\angle DAB°\)
\(=180°-90°-\angle DAB°\)
\(=90°-\angle DAB°\) ・・・③
一直線の角は\(180°\) なので②より、
\(\angle CAE=180°-\angle CAB-\angle DAB°\)
\(=180°-90°-\angle DAB°\)
\(=90°-\angle DAB°\) ・・・④
③、④より、
\(\angle ABD=\angle CAE\) ・・・⑤
①、②、⑤より、直角三角形の斜辺と他の \(1\) つの鋭角がそれぞれ等しいので
\(\triangle ABD \equiv \triangle CAE\)
