1次式の計算
分配法則を用いて、\(1\) 次式の加減を計算します。
符号がどうなるのか、迷ってしまう人が出やすい単元です。
まずは意味を考えることより、計算ができることが大事です。
計算ルールを覚えて、機械的に処理できるようになることを優先しましょう。
1次式を足す、引く
次の計算をしなさい。
① \(4a+3(a+2)\)
② \(4a+3(a-2)\)
③ \(4a-3(a+2)\)
④ \(4a-3(a-2)\)
解説
正を引いているのか、負を足しているのか・・
そのような意味を考えることよりも、
ただただ、計算ルールにしたがって計算していまいましょう。
かけ算の答え(積)をただ並べる方式でスッキリ解決です。
① \(4a+3(a+2)\)
正の符号だけなので、迷わず計算できますね。
\(4a+3(a+2)\)
\(=4a+3a+6\) ・・・( )をはずした
\(=7a+6\) ・・・同類項をまとめた
② \(4a+3(a-2)\)
負の符号があるときに混乱が起きやすいのですが、
下図のような、「ただ並べる方式」で計算しましょう。
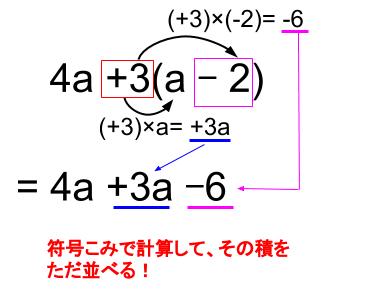
\(4a+3(a-2)\)
\(=4a+3a-6\)
\(=7a-6\)
③ \(4a-3(a+2)\)
負の符号がありますが、
下図のような、「ただ並べる方式」で計算すれば問題なしです。
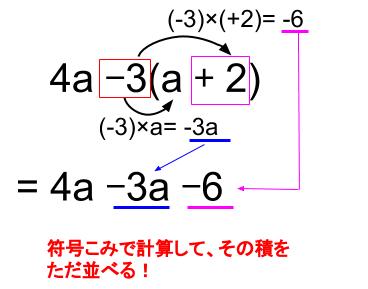
\(4a-3(a+2)\)
\(=4a-3a-6\)
\(=a-6\)
④ \(4a-3(a-2)\)
同じく負の符号がありますが、
下図のような、「ただ並べる方式」で計算すれば問題なしです。
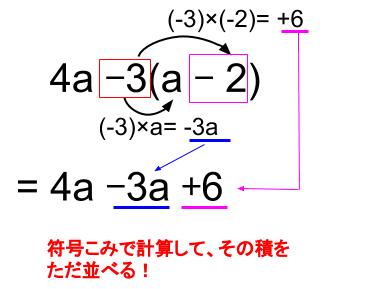
\(4a-3(a-2)\)
\(=4a-3a+6\)
\(=a+6\)
「並べる方式」は万能の計算方法
次の計算をしなさい。
① \(5-(-2)\)
② \(30-6×(-2)\)
解説
学習初期に、意味を考えながら計算をしたものです。
これらも、「ただ積を並べる方式」で容易に計算可能です。
① \(5-(-2)=5+2=7\)

※学習初期は、負の数 \(-2\) を引くとはどのような意味なのかを考察しました。
② \(30-6×(-2)=30+12=42\)

※学習初期は、\(30\) から \(6×(-2)\) を引く
という計算をしました。もちろん、今この計算をしてもまったく間違いではありません。
\(30-6×(-2)\)
\(=30-\underline{6×(-2)}\)
\(=30-\underline{(-12)}\)
\(=30+12\)
\(=42\)
でも、「ただ並べる方式」が圧倒的に速いですね。
例題
次の計算をしなさい。
① \(3(x-2)-2(x+2)\)
② \(\displaystyle \frac{a-3}{2}-\displaystyle \frac{2a-1}{3}\)
解説
① 「ただ並べる方式」で行きましょう。
\(3(x-2)-2(x+2)\)
\(=3x-6-2x-4\)
\(=x-10\)
② 通分します。ていねいに途中式を書いていきましょう。
\(\displaystyle \frac{a-3}{2}-\displaystyle \frac{2a-1}{3}\)
\(=\displaystyle \frac{3(a-3)}{6}-\displaystyle \frac{2(2a-1)}{6}\)
\(=\displaystyle \frac{3a-9}{6}-\displaystyle \frac{4a-2}{6}\)
\(=\displaystyle \frac{3a-9-(4a-2)}{6}\) ・・・引くほうの分子に( )をつける!!
\(=\displaystyle \frac{3a-9-4a+2}{6}\)
\(=\displaystyle \frac{-a-7}{6}\) ・・・これを最終結果としても間違いではない。
\(=-\displaystyle \frac{a}{6}-\displaystyle \frac{7}{6}\)
スポンサーリンク
