円すいの展開図
円すいの展開図は、下図のようになります。
側面を切り開いたおうぎ形と底面の円からなります。

側面のおうぎ形の中心角は、以下の公式から求めることができます。
円すいの側面の中心角= \(360×\)\(\displaystyle \frac{底面の半径}{母線}\)
また、側面の面積=側面積の公式もあります。
円すいの側面積=\(母線×底面の半径×{\pi}\)
まずはこの2つの公式をしっかり覚えてしまいましょう。
中心角の公式の成り立ち
なぜ円すいの2つの公式が成立するのでしょうか。
まず第一に、下図の赤線の長さが等しいということです。
これは、「組み立てたらぴったりだから」ということで、
計算によって求めることではありません。
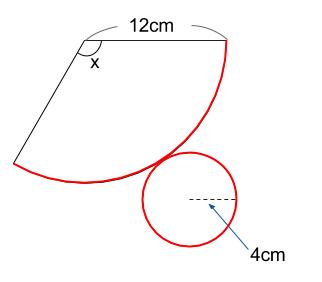
つまり、
側面のおうぎ形の弧の長さ = 底面の円周
なので、側面のおうぎ形の中心角を \(x\) とすると、
\(母線×2×{\pi}×\displaystyle \frac{x}{360}=底面の半径×2×{\pi}\)
が成り立ちます。
この等式を変形していくと、中心角の公式が得られます。
両辺を \(2{\pi}\) で割ると
\(母線×\displaystyle \frac{x}{360}=底面の半径\)
両辺を母線でわると
\(\displaystyle \frac{x}{360}=\displaystyle \frac{底面の半径}{母線}\) ・・・ これは大事な比
両辺に \(360\) をかけると
\(x=360×\displaystyle \frac{底面の半径}{母線}\)
これこそが中心角の公式でですね。
続いて側面積の公式を導きます。
側面積の公式の成り立ち
次に、円すいの側面積の公式を導きましょう。
円すいの側面積は、半径が母線のおうぎ形なので、
\(側面積=母線×母線×{\pi}×\displaystyle \frac{x}{360}\)
ですが、\(\displaystyle \frac{x}{360}=\displaystyle \frac{底面の半径}{母線}\)
でしたので、これを代入すると、
\(側面積=母線×母線×{\pi}×\displaystyle \frac{x}{360}\)
\(=母線×母線×{\pi}×\displaystyle \frac{底面の半径}{母線}\)
\(=母線×{\pi}×底面の半径\)
と求まります。
側面積の公式が導けました。
スポンサーリンク
