歯車は反比例
かみあった歯車が回転する問題があります。
これは反比例の問題ですし、
反比例のときにしか「歯車」もでてきません。
覚えてしまいましょう。
例題
歯車 \(A\) があり、その歯数は \(30\) で、\(1\) 分間に \(10\) 回転します。
この歯車 \(A\) に、いろいろな歯車をかみ合わせて回転させます。
歯車 \(A\) にかみ合わせる歯車を歯車 \(B\) とし、その歯数を \(x\) 、
\(1\) 分間の回転数を \(y\) とするとき、次の問いに答えなさい。
① \(x=50\) のときの \(y\) を求めなさい。
② \(y\) を \(x\) の式で表しなさい。
解説
「かみあった歯車が回転」するとき、何が起こるのか説明します。
下図の赤色の部分に注目します。
\(1\) 分間 \(2\) つの歯車を回転させたとき、
この部分を、のべいくつの歯が通過したのかを考えます。
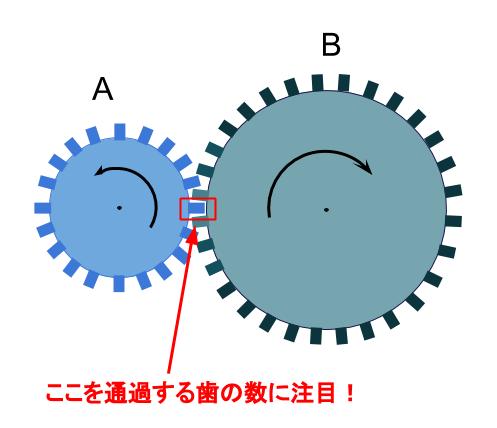
※図は、不正確です。念のため。
歯車 \(A\) と歯車 \(B\) はかみ合っているので、
赤部分を通過する歯は、
\(A\) の歯 → \(B\) の歯 → \(A\) の歯 → \(B\) の歯 → ・・・
と交互に規則正しくなります。
つまり、
「\(A\) の歯が赤部分を通過した回数」
と
「\(B\) の歯が赤部分を通過した回数」
は等しくなります。
※現実世界では回転させた時間しだいでは、どちらかが \(1\) 回多くなることもあるでしょうが、数学の問題において、それは考慮する必要はありません。
①\(x=50\) のときの \(y\)
歯車 \(A\) の歯数は \(30\) で、\(1\) 分間に \(10\) 回転するので、
\(30×10=300\) より、
歯車 \(A\) の歯は \(1\) 分間に、のべ \(300\) 、赤部分を通過します。
※歯の数を数える単位は何でしょう?枚でしょうか?
とりあえず単位なしで話を進めます。
一方
歯車 \(B\) の歯数は \(50\) で、\(1\) 分間に \(y\) 回転するので、
\(50×y=300\) より、
\(y=6\)
です。
※ \(B\) は \(1\) 分間に \(6\) 回転するということです。
②\(y\) を \(x\) の式で表せ
\(Aの歯数×Aの回転数=Bの歯数×Bの回転数\)
が成立します。
※これを覚えてしまいましょうね。
\(A\) の歯数 \(30\)
\(A\) の \(1\) 分間の回転数 \(10\) をこの式に入れると
\(30×10=xy\)
より、
\(y=\displaystyle \frac{300}{x}\)
となります。
これが求める式です。
かみ合う歯車のまとめ
かみ合う歯車 \(A,B\) に関して、
\(Aの歯数×Aの回転数=Bの歯数×Bの回転数\)
が成立します。
これを覚えましょう。
積一定なので、反比例の関係です。
反比例なので、
\(y=\displaystyle \frac{a}{x}\)
という式になるのですが、
歯車の問題を解くときは、
\(Aの歯数×Aの回転数=Bの歯数×Bの回転数=比例定数 a\)
で解くのがおススメです。
式成立の意味がわかるので、圧倒的に覚えやすいです。
必要に応じて、
\(y=\displaystyle \frac{a}{x}\)
の形に式変形をすれば良いのです。
スポンサーリンク
